
题目列表(包括答案和解析)
1.已知集合M={x|x<3},N={x|log2x>1},则M∩N=
A. 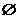 B.{x|0<x<3} C.{x|1<x<3} D.{x|2<x<3}
B.{x|0<x<3} C.{x|1<x<3} D.{x|2<x<3}
19. 已知函数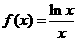 .
.
(Ⅰ)求函数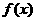 的单调区间及其极值;
的单调区间及其极值;
(Ⅱ)证明:对一切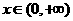 ,都有
,都有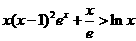 成立.
成立.
20 在数列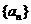 中,
中,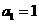 ,且
,且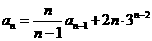
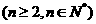 .
.
(Ⅰ)求数列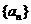 的通项公式;
的通项公式;
(Ⅱ)令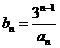
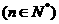 ,数列
,数列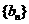 的前
的前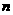 项和为
项和为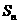 ,试比较
,试比较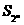 与
与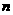 的大小;
的大小;
(Ⅲ)令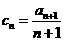
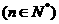 ,数列
,数列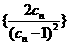 的前
的前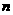 项和为
项和为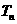 ,求证:对任意
,求证:对任意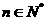 都有
都有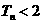
18. 已知两点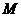 和
和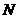 分别在直线
分别在直线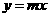 和
和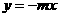
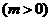 上运动,且
上运动,且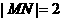 ,动点
,动点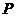 满足:
满足: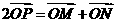 (
( 为坐标原点),点
为坐标原点),点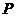 的轨迹记为曲线
的轨迹记为曲线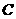 .
.
(Ⅰ)求曲线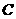 的方程,并讨论曲线
的方程,并讨论曲线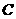 的类型;
的类型;
(Ⅱ)过点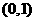 作直线
作直线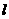 与曲线
与曲线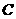 交于不同的两点
交于不同的两点 、
、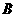 ,若对于任意
,若对于任意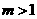 ,都有
,都有 为锐角,求直线
为锐角,求直线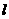 的斜率
的斜率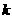 的取值范围.
的取值范围.
17. 某种家用电器每台的销售利润与该电器的无故障使用时间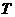 (单位:年)有关。若
(单位:年)有关。若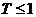 ,则销售利润为
,则销售利润为 元;若
元;若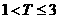 ,则销售利润为
,则销售利润为 元;若
元;若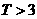 ,则销售利润为
,则销售利润为 元.设每台该种电器的无故障使用时间
元.设每台该种电器的无故障使用时间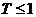 ,
,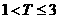 及
及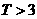 这三种情况发生的概率分别为
这三种情况发生的概率分别为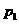 ,
,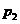 ,
,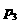 ,叉知
,叉知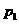 ,
,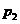 是方程
是方程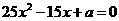 的两个根,且
的两个根,且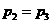
(1)求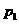 ,
,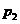 ,
,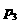 的值;
的值;
(2)记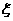 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求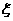 的期望.
的期望.
16.如图,在长方体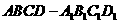 中,
中,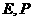 分别是
分别是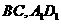 的中点,M、N分别是
的中点,M、N分别是
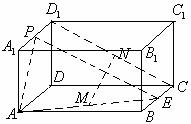
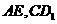 的中点,
的中点,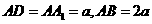
(1)求证: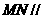 面
面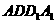
(2)求三棱锥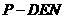 的体积
的体积
15. 在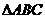 中,
中,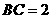 ,
,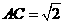
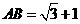 .
.
(Ⅰ)求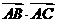 ;
;
(11)设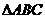 的外心为
的外心为 ,若
,若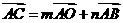 ,求
,求 ,
,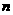 的值.
的值.
14.已知一容器中有A、B两种菌,且在任何时刻A、B两种菌的个数乘积为定值1010。为了简单起见,科学家用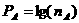 来记录A菌个数的资料,其中
来记录A菌个数的资料,其中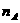 为A菌的个数。则下列判断中正确的个数为
个。
为A菌的个数。则下列判断中正确的个数为
个。
①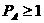
②若今天的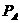 值比明天的
值比明天的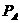 值增加1,则今天的A菌个数比昨天的A菌个数多了10个
值增加1,则今天的A菌个数比昨天的A菌个数多了10个
③假设科学家将B菌的个数控制为5万个,则此时5<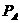 <5.5
<5.5
13. 函数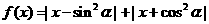
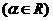 的最小值是
.
的最小值是
.
12. .设动直线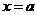 与函数
与函数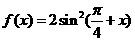 和
和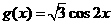 的图象分别交于
的图象分别交于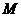 、
、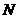 两点,则
两点,则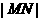 的最大值为 .
的最大值为 .
11.某地为了了解该地区10000户家庭的用电
情况,采用分层抽样的方法抽取了500户
家庭的月平均电用量,并根据这500户家
庭月平均用量画出频率分布直方图(如图),
则该地区1000户家庭中月平均用电度数
在[70,80]的家庭有 户。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com