
题目列表(包括答案和解析)
3.在平面直角坐标系中,已知点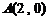 、
、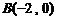 ,
,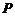 是平面内一动点,直线
是平面内一动点,直线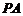 、
、 的斜率之积为
的斜率之积为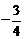 .
.
(Ⅰ)求动点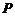 的轨迹
的轨迹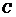 的方程;
的方程;
(Ⅱ)过点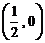 作直线
作直线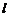 与轨迹
与轨迹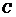 交于
交于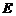 、
、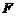 两点,线段
两点,线段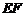 的中点为
的中点为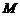 ,求直线
,求直线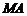 的斜率
的斜率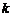 的取值范围.
的取值范围.
2.已知直线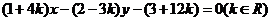 所经过的定点
所经过的定点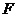 恰好是椭圆
恰好是椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 上的点到点
上的点到点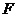 的最大距离为8.
的最大距离为8.
(Ⅰ)求椭圆 的标准方程;(7分)
的标准方程;(7分)
(Ⅱ)已知圆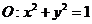 ,直线
,直线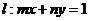 .试证明当点
.试证明当点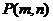 在椭圆
在椭圆 上运动时,直线
上运动时,直线 与圆
与圆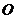 恒相交;并求直线
恒相交;并求直线 被圆
被圆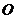 所截得的弦长的取值范围. (8分)
所截得的弦长的取值范围. (8分)
1.已知:以点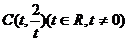 为圆心的圆与
为圆心的圆与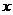 轴交于点
轴交于点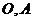 ,与
,与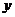 轴交于点
轴交于点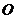 、
、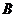 ,其中
,其中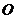 为原点。求证:
为原点。求证: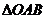 的面积为定值;
的面积为定值;
(1) 设直线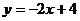 与圆
与圆 交于点
交于点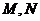 ,若
,若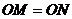 ,求圆
,求圆 的方程。
的方程。
5.已知平面区域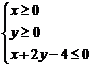 恰好被面积最小的圆
恰好被面积最小的圆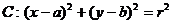 及其内
及其内
部所覆盖.
(Ⅰ)试求圆 的方程.
的方程.
(Ⅱ)若斜率为1的直线 与圆C交于不同两点
与圆C交于不同两点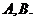 满足
满足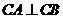 ,求直线
,求直线 的方程.
的方程.
赣马高级中学解答题专题训练19
解析几何(二) 编写:刘建自 审核:王怀学
4.已知与曲线C: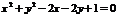 相切的直线
相切的直线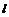 交
交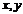 的正半轴与
的正半轴与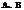 两点,O为原点,
两点,O为原点,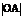 =a,
=a,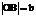 ,
,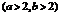 .
.
(1)求线段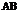 中点的轨迹方程;(2)求
中点的轨迹方程;(2)求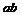 的最小值.
的最小值.
3.已知直线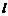 :y=k(x+2
:y=k(x+2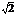 )与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
(1)试将S表示成k的函数,并求出它的定义域;(2)求S的最大值,并求取得最大值时k的值.
2.已知P(2,0),Q(8,0),点M到点P的距离是它到点Q距离的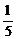 ,求点M的轨迹方程,并求轨迹上的点到直线l:8x-y-1=0的最小距离.
,求点M的轨迹方程,并求轨迹上的点到直线l:8x-y-1=0的最小距离.
1.过点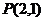 作直线
作直线 分别交
分别交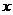 轴的正半轴和y轴的正半轴于点
轴的正半轴和y轴的正半轴于点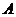 、
、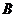 ,当
,当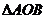 (
(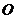 为原点)的面积
为原点)的面积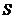 最小时,求直线
最小时,求直线 的方程,并求出
的方程,并求出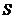 的最小值.
的最小值.
6.数列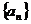 的前n项和记为
的前n项和记为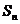 ,已知
,已知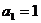 ,
,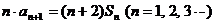
(1)证明数列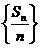 是公比为2的等比数列。(2)求
是公比为2的等比数列。(2)求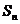 关于n的表达式。
关于n的表达式。
(3)请猜测是否存在自然数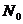 ,对于所有的
,对于所有的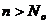 有
有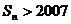 恒成立,并证明。
恒成立,并证明。
解:(1)∵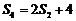 ,∴
,∴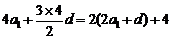 解得
解得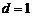
(2)∵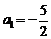 ,∴数列
,∴数列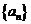 的通项公式为
的通项公式为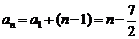 ∴
∴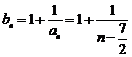
∵函数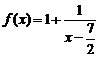 在
在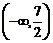 和
和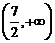 上分别是单调减函数,
上分别是单调减函数,
∴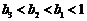 当
当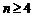 时,
时,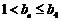 ∴数列
∴数列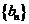 中的最大项是
中的最大项是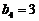 ,最小项是
,最小项是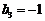
(2)由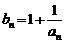 得
得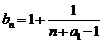 又函数
又函数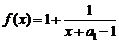 在
在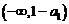 和
和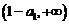 上分别是单调减函数,且
上分别是单调减函数,且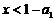 时
时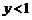 ;
;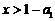 时
时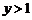 .
.
∵对任意的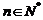 ,都有
,都有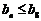 ,∴
,∴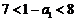 ∴
∴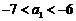
∴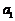 的取值范围是
的取值范围是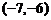
5.如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.(1)设AD=x(x≥0),ED=y,求用x表示y的函数关系式;
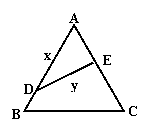 (2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
解:(1)在△ADE中,y2=x2+AE2-2x·AE·cos60° y2=x2+AE2-x·AE,①
y2=x2+AE2-x·AE,①
又S△ADE=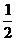 S△ABC=
S△ABC=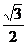 a2=
a2=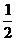 x·AE·sin60°
x·AE·sin60° x·AE=2.②
x·AE=2.②
②代入①得y2=x2+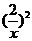 -2(y>0), ∴y=
-2(y>0), ∴y=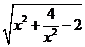 (1≤x≤2).
(1≤x≤2).
(2)如果DE是水管y=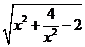 ≥
≥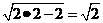 ,
,
当且仅当x2=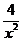 ,即x=
,即x=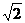 时“=”成立,故DE∥BC,且DE=
时“=”成立,故DE∥BC,且DE=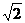 .
.
如果DE是参观线路,记f(x)=x2+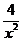 ,可知函数在[1,
,可知函数在[1,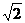 ]上递减,在[
]上递减,在[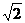 ,2]上递增,故f(x) max=f(1)=f(2)=5. ∴y max=
,2]上递增,故f(x) max=f(1)=f(2)=5. ∴y max=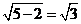 .即DE为AB中线或AC中线时,DE最长.
.即DE为AB中线或AC中线时,DE最长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com