
题目列表(包括答案和解析)
22.(本小题满分12分)
等差数列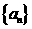 中,
中,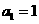 ,
,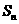 为其前n项和,等比数列
为其前n项和,等比数列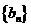 的公比q满足
的公比q满足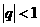 ,
,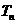 为其前n项和,若
为其前n项和,若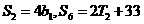 又
又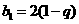
(1)求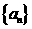 、
、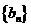 的通项公式;
的通项公式;
(2)若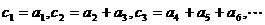 ,求
,求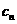 的表达式;
的表达式;
(3)若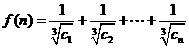 ,求证
,求证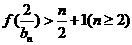 。
。
21.(本小题满分12分)
已知以向量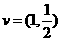 为方向向量的直线
为方向向量的直线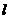 过点
过点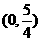 ,抛物线
,抛物线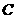 :
: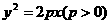 的顶点关于直线
的顶点关于直线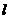 的对称点在该抛物线的准线上.
的对称点在该抛物线的准线上.
(1) 求抛物线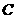 的方程;
的方程;
(2) 设 、
、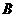 是抛物线
是抛物线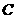 上的两个动点,过
上的两个动点,过 作平行于
作平行于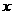 轴的直线
轴的直线 ,直线
,直线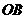 与直线
与直线 交于点
交于点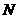 ,若
,若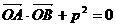 (
( 为坐标原点,
为坐标原点, 、
、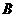 异于点
异于点 ),试求点
),试求点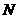 的轨迹方程。
的轨迹方程。
20.(本小题满分12分)
已知函数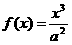 图象上斜率为3的两条切线间的距离为
图象上斜率为3的两条切线间的距离为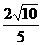 ,函数
,函数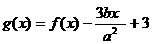 .
.
(1)若函数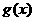 在
在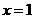 处有极值,求
处有极值,求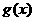 的解析式;
的解析式;
(2 ) 若函数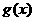 在区间
在区间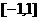 上为增函数,且
上为增函数,且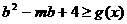 在区间
在区间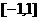 上都成立,求实数
上都成立,求实数 的取值范围.
的取值范围.
19.(本小题满分12分)
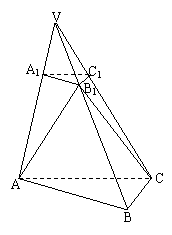 如图,己知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边三角形AB1C所在平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a,
如图,己知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边三角形AB1C所在平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a,
(1)求证:直线B1C1为异面直线AB1与A1C1的公垂线;
(2)求A到平面VBC的距离;
(3)求二面角A-VB-C大小。
18.(本小题满分12分)
甲、乙两位篮球运动员进行定点投蓝,每人各投4个球,甲投篮命中的概率为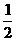 ,乙投篮命中的概率为
,乙投篮命中的概率为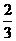 .
.
(1)求甲至多命中2个且乙至少命中2个的概率;
(2)若规定每投篮一次命中得3分,未命中得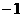 分,求乙所得分数
分,求乙所得分数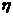 的概率分布和数学期望.
的概率分布和数学期望.
17.(本小题满分10分)
已知向量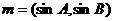 ,
,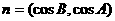 ,
,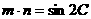 ,且A、B、C分别为
,且A、B、C分别为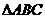 的三边所对的角。
的三边所对的角。
(1)求角C的大小;
(2)若三边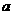 、
、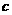 、
、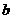 成等差数列,且
成等差数列,且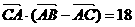 ,求边
,求边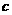 的长。
的长。
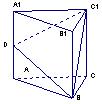
16、如图,在正三棱柱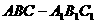 中,D为棱
中,D为棱 的中点,若截面
的中点,若截面 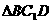 是面积为6的直角三角形,则此三棱柱的体积为
。
是面积为6的直角三角形,则此三棱柱的体积为
。
15.若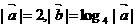 且
且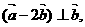 ,则向量
,则向量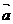 与向量
与向量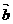 的夹角是_________。
的夹角是_________。
14.已知数列{an}的前n项和Sn是二项式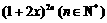 展开式中含x奇次幂的系数和,
则数列{an}的通项公式an=--------。
展开式中含x奇次幂的系数和,
则数列{an}的通项公式an=--------。
13.已知平面区域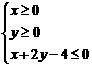 恰好被面积最小的圆
恰好被面积最小的圆 及其内部所覆盖.则圆
及其内部所覆盖.则圆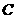 的方程为
。
的方程为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com