
题目列表(包括答案和解析)
6.(本题满分14分)
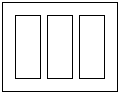
迎世博,要设计如图的一张矩形广告,该广告含有大小相等的左中右三个矩形栏目,这三栏的面积之和为 ,四周空白的宽度为
,四周空白的宽度为 ,栏与栏之间的中缝空白的宽度为
,栏与栏之间的中缝空白的宽度为 ,怎样确定广告矩形栏目高与宽的尺寸(单位:
,怎样确定广告矩形栏目高与宽的尺寸(单位: ),能使整个矩形广告面积最小.
),能使整个矩形广告面积最小.
5.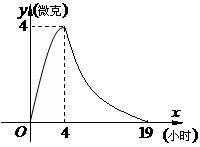 某医药研究所开发一种新药,据监测:服药后每毫升血液中的含药量
某医药研究所开发一种新药,据监测:服药后每毫升血液中的含药量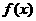 与时间
与时间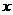 之间满足如图所示曲线.当
之间满足如图所示曲线.当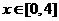 时,所示的曲线是二次函数图像的一部分,满足
时,所示的曲线是二次函数图像的一部分,满足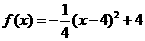 ,当
,当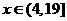 时,所示的曲线是函数
时,所示的曲线是函数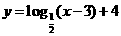 的图像的一部分.据测定:每毫升血液中含药量不少于
的图像的一部分.据测定:每毫升血液中含药量不少于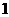 微克时治疗疾病有效.请你算一下,服用这种药一次大概能维持多长的有效时间?(精确到
微克时治疗疾病有效.请你算一下,服用这种药一次大概能维持多长的有效时间?(精确到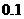 小时)
小时)
4.(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知函数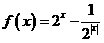 .
.
(1)(理)设集合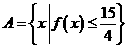 ,
,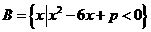 ,若
,若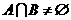 ,求实数
,求实数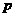 的取值范围;
的取值范围;
(文)若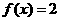 ,求
,求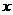 的值;
的值;
(2)若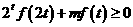 对于
对于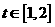 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
3.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
某商品每件成本价80元,售价100元,每天售出100件.若售价降低x成(1成=10%),售出商品数量就增加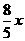 成,要求售价不能低于成本价.
成,要求售价不能低于成本价.
(1)设该商店一天的营业额为y,试求y与x之间的函数关系式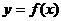 ,并写出定义域;
,并写出定义域;
(2)若再要求该商品一天营业额至少10260元,求x的取值范围.
2.(本题满分14分,第1小题6分,第2小题8分)
已知关于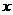 的不等式
的不等式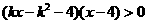 ,其中
,其中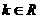 .
.
(1)当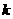 变化时,试求不等式的解集
变化时,试求不等式的解集 ;
;
(2)对于不等式的解集 ,若满足
,若满足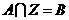 (其中
(其中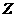 为整数集). 试探究集合
为整数集). 试探究集合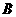 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合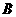 中元素个数最少的
中元素个数最少的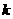 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合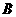 ;若不能,请说明理由.
;若不能,请说明理由.
1.(本题满分10分)
解不等式: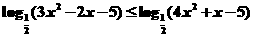 .
.
15.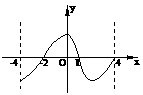 设函数
设函数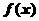 的定义域为
的定义域为 ,其图像如下图,那么不等式
,其图像如下图,那么不等式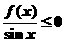 的解集为____________.
的解集为____________.
14.研究问题:“已知关于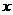 的不等式
的不等式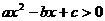 的解集为
的解集为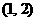 ,解关于
,解关于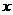 的不等式
的不等式
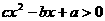 ”,有如下解法:
”,有如下解法:
 解:由
解:由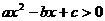
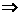
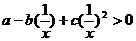 ,令
,令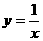 ,则
,则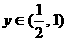 ,
,
所以不等式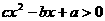 的解集为
的解集为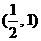 .
.
参考上述解法,已知关于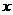 的不等式
的不等式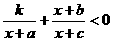 的解集为
的解集为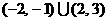 ,则
,则
关于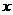 的不等式
的不等式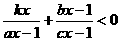 的解集为
.
的解集为
.
13.关于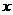 的方程
的方程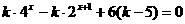 在区间
在区间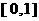 上有解,则实数
上有解,则实数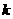 的取值范围是
.
的取值范围是
.
12.无穷等比数列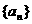 各项和
各项和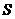 的值为2,公比
的值为2,公比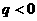 ,则首项
,则首项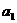 的取值范围是 .
的取值范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com