
题目列表(包括答案和解析)
2.
已知命题P: 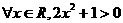 .则(
)
.则(
)
A.
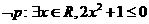 B.
B. 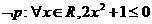
C. 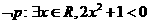 D.
D. 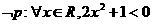
1. 设全集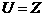 ,集合
,集合 ,
,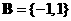 ,则
,则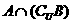 =( )
=( )
A. 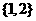 B.
B.
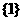 C.
C. 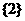 D.
D.
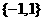
22.(14分)对于函数f(x),若存在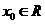 ,使得
,使得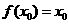 成立,则称
成立,则称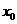 为f(x)的不动点,已知函数
为f(x)的不动点,已知函数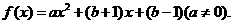
(1)当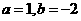 时,求函数f(x)的不动点;
时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在⑵条件下,若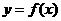 图象上的A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线
图象上的A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线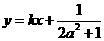 对称,求b 的最小值.
对称,求b 的最小值. 

21.(12分)已知f(x)、g(x)是定义在[a,b]上的函数,若对任意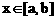 ,总有
,总有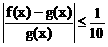 ,则称f(x)可被g(x)替代,试判断函数
,则称f(x)可被g(x)替代,试判断函数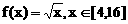 能否被
能否被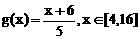 替代,并说明理由.
替代,并说明理由. 

20.(12分)已知函数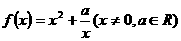
(1)判断函数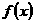 的奇偶性;
的奇偶性;
(2)若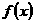 在区间
在区间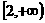 是增函数,求实数
是增函数,求实数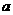 的取值范围.
的取值范围. 

19.(12分)设函数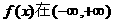 上满足
上满足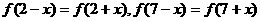 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有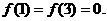


(1)试判断函数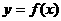 的奇偶性;
的奇偶性;
(2)试求方程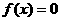 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.
18.(12分)某蔬菜基地种植番茄,由历年市场行情得知,从二月一日起的300天内,番茄市场售价与上市时间的关系用图(1)的一条折线表示;番茄的种植成本与上市时间的关系用图(2)的抛物线表示.
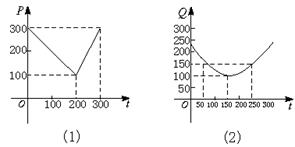
(1)写出图1表示的市场售价与时间的函数关系式P=f(t);图2表示的种植成本与时间的函数关系式Q=g(t);
(2)市场售价减去种植成本为纯收益,问何时上市的番茄纯收益最大?(注:市场售价和种植成本的单位:元/102 ,kg,时间单位:天)
17.(12分) 已知函数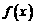 和
和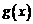 的图象关于原点对称,且
的图象关于原点对称,且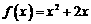 .
.
(1)求函数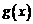 的解析式;
的解析式;
(2)解不等式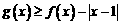 ;
;
16.给出下列命题:
①不存在实数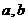 使
使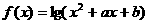 的定义域、值域均为一切实数;
的定义域、值域均为一切实数;
②函数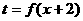 图象与函数
图象与函数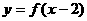 图象关于直线
图象关于直线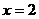 对称;
对称;
③函数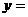
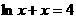 有且只有一个实数根;
有且只有一个实数根;
④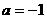 是方程
是方程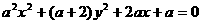 表示圆的充分必要条件.
表示圆的充分必要条件.
其中真命题的序号是______________________.(写出所有真命题的序号)
15.定义在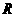 上的奇函数
上的奇函数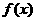 和偶函数
和偶函数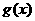 满足
满足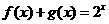 ,则
,则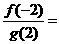 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com