14. 某地区预计从2005年初的前n个月内，对某种商品的需求总量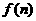(万件)与月份n的近似关系为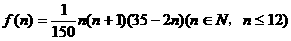

　　 (I)求2005年第n个月的需求量g(n)(万件)与月份n的函数关系式，并求出哪个月份的需求量超过1.4万件。

　　 (II)如果将该商品每月都投放市场P万件，要保持每月都满足供应，则P至少为多少万件？

13. 一个有140名职工的合资企业投资生产甲、乙两种不同产品，2000年该企业生产的甲产品创外汇32万元，乙产品创外汇216万元，该企业以后每年所创外汇是甲产品以2.25倍的速度递增，而生产乙产品的机器由于老化的原因，每年创外汇为上年的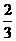。这个企业只要年人均创外汇达3万元就可以列入国家重点企业。若以2000为第一年，问：

(Ⅰ)从哪一年开始，甲产品年创外汇超过乙产品年创外汇(lg2=0.3010,lg3=0.4771)

(Ⅱ)该企业哪一年所创外汇最少？该年甲、乙两种产品各创外汇多少万元？

(Ⅲ)该企业到2003年能否进入国家重点企业？

12. 某渔业公司今年初用98万购进一艘渔船用于捕捞.第一年需各种费

　　 用12万元，从第二年开始每年包括维修费在内，所需费用均比上一年增加4万元，该船捕捞总收入预计每年50万元.

1)　 该船捕捞几年开始盈利(即总收入减去成本及所有费用之差为正)？

2)　 该船捕捞若干年后，处理方案有两种：

① 年平均盈利达到最大值时，以26万元的价格卖出；

② 盈利总额达到最大时，以8万元的价格卖出.

　　　　 问哪一种方案较为合算？并说明理由.

11. 已知水渠在过水断面面积为定值的情况下，过水湿周越小，其流量越大．

　现有以下两种设计，如图：

　图①的过水断面为等腰△ABC，AB＝BC，过水湿周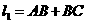．图②的过水断面为等腰梯形ABCD，AB＝CD，AD∥BC，∠BAD＝60°，过水湿周．

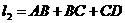　若△ABC与梯形ABCD的面积都为S，

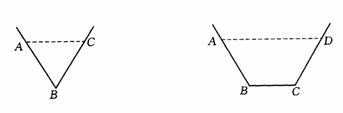
　　　　　 图①　　　　　　 　图②

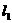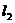　(1)分别求和的最小值；

　(2)为使流量最大，给出最佳设计方案．

10. 某工厂去年的某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元．今年，工厂第一次投入100万元(科技成本)，并计划以后每年比上一年多投入100万元(科技成本)，预计产量年递增10万只，第n次投入后，每只产品的固定成本为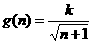(k＞0，k为常数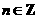，且n≥0)，若产品销售价保持不变，第n次投入后的年利润为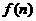万元．

　(1)求k的值，并求出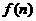的表达式；

　(2)问从今年算起第几年利润最高?最高利润为多少万元?

9. 已知如图, 某海滨浴场的岸边可近似地看成直线, 位于岸边A处的救生员发现海中B处有人求救, 救生员尚有直接从A处游向B处, 而是沿岸边自A跑到距离B最近的D处, 然后游向B处,若救生员在岸边的行进速度为6米/秒,在海中的行进速度为2米/秒.

(I) 分析救生员的选择是否正确;

(II) 有AD上找一点C, 使救生员从A到B的时间为最短,并求出最短时间.　　　　　　　

　　　　　　　　　　　　　　　 B

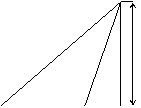
　　　　　　　　　　　　　　　　　 300米

　　　　　 A　　　　　　 C　　　 D

8. 设某旅游景点每天的固定成本为500元，门票每张为30元，变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时，该旅游景点收支平衡；一天购票人数超过100时，该旅游景点须另交保险费200元。设每天的购票人数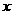为，盈利额为。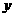

(Ⅰ)求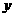与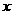之间的函数关系； (Ⅱ)试用程序框图描述算法(要求：输入购票人数，输出盈利额)；

(Ⅲ)该旅游景点希望在人数达到20人时即不出现亏损，若用提高门票价格的措施，则每张门票至少要多少元(取整数)？ 　注：可选用数据：.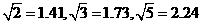

7. 随着我国加入WTO，某企业决定从甲、乙两种产品中选择一种进行投资生产，打入国际市场。已知投资生产这两种产品的有关数据如下表(单位：万美元)

项 目 类　 别	年固定成本	每件产品成本	每件产品销售价	每年最多生产的件数
甲产品	30	a	10	200
乙产品	50	8	18	120

　其中年固定成本与生产的件数无关，a为常数，且4≤a≤8。令外，年销售x件乙产品时需上交0.05x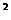万美元的特别关税。

(1)　 写出该厂分别投资生产甲、乙两种产品的年利润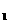y,y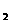与生产相应产品的件数x (x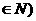之间的函数关系式；

(2)　 分别求出投资生产这两种产品的最大年利润；

(3)　 如何决定投资可获最大年利润。

6. 某企业甲将经营状态良好的某种消费品专卖店以58万元的　　

　　 优惠价转让给企业乙，约定乙用经营该店的利润偿还转让费(不计息)。已知经营

　　 该店的固定成本为6.8万元/月，该消费品的进价为16元/件，月销量q(万件)

　　 与售价p(元/件)的关系如图.

　 (1)写出销量q与售价p的函数关系式；

　　 　 (2)当售价p定为多少时，月利润最多？

　　 　 (3)企业乙最早可望在经营该专卖店几

　　　　　 个月后还清转让费？

5. 如图，某海滨浴场的岸边可近似的看成直线，位于岸边A处的救生员发现海中B处有人求救，救生员没有直接从A处游向B处，而沿岸边自A跑到距离B最近的D处，然后游向B处，若救生员在岸边的行速为6米/秒，在海中的行进速度为2米/秒，

⑴分析救生员的选择是否正确；

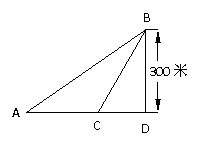⑵在AD上找一点C，是救生员从A到B的时间为最短，并求出最短时间。