
题目列表(包括答案和解析)
2.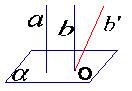 线面垂直
线面垂直
定义:如果一条直线l和一个平面α相交,并且和平面α内的任意一条直线都垂直,我们就说直线l和平面α互相垂直其中直线l叫做平面的垂线,平面α叫做直线l的垂面,直线与平面的交点叫做垂足。直线l与平面α垂直记作:l⊥α。
直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
1.线线垂直
判断线线垂直的方法:所成的角是直角,两直线垂直;垂直于平行线中的一条,必垂直于另一条。
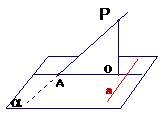 三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那麽它也和这条斜线的射影垂直
推理模式: 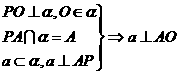 。
。
注意:⑴三垂线指PA,PO,AO都垂直α内的直线a 其实质是:斜线和平面内一条直线垂直的判定和性质定理⑵要考虑a的位置,并注意两定理交替使用。
近年来,立体几何高考命题形式比较稳定,题目难易适中,常常立足于棱柱、棱锥和正方体,复习是要以多面体为依托,始终把直线与直线、直线与平面、平面与平面垂直的性质和判定作为考察重点。在难度上也始终以中等偏难为主,在新课标教材中将立体几何要求进行了降低,重点在对图形及几何体的认识上,实现平面到空间的转化,示知识深化和拓展的重点,因而在这部分知识点上命题,将是重中之重。
预测2010年高考将以多面体为载体直接考察线面位置关系:
(1)考题将会出现一个选择题、一个填空题和一个解答题;
(2)在考题上的特点为:热点问题为平面的基本性质,考察线线、线面和面面关系的论证,此类题目将以客观题和解答题的第一步为主。
(3)解答题多采用一题多问的方式,这样既降低了起点又分散了难点
以立体几何的上述定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中线面垂直的有关性质与判定。
通过直观感知、操作确认,归纳出以下判定定理:
◆一条直线与一个平面内的两条相交直线垂直,则该直线与此平面垂直。
◆ 一个平面过另一个平面的垂线,则两个平面垂直。
通过直观感知、操作确认,归纳出以下性质定理,并加以证明:
◆两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
能运用已获得的结论证明一些空间位置关系的简单命题。
2.空间的距离问题,主要是求空间两点之间、点到直线、点到平面、两条异面直线之间(限于给出公垂线段的)、平面和它的平行直线、以及两个平行平面之间的距离.
求距离的一般方法和步骤是:一作--作出表示距离的线段;二证--证明它就是所要求的距离;三算--计算其值.此外,我们还常用体积法求点到平面的距离.
求空间中线面的夹角或距离需注意以下几点:
①注意根据定义找出或作出所求的成角或距离,一般情况下,力求明确所求角或距离的位置.
②作线面角的方法除平移外,补形也是常用的方法之一;求线面角的关键是寻找两“足”(斜足与垂足),而垂足的寻找通常用到面面垂直的性质定理.
③求二面角高考中每年必考,复习时必须高度重视.二面角的平角的常用作法有三种:
根据定义或图形特征作;根据三垂线定理(或其逆定理)作,难点在于找到面的垂线.解决办法,先找面面垂直,利用面面垂直的性质定理即可找到面的垂线;作棱的垂面。作二面角的平面角应把握先找后作的原则.此外在解答题中一般不用公式“cosθ=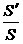 ”求二面角否则要适当扣分。
”求二面角否则要适当扣分。
④求点到平面的距离常用方法是直接法与间接法,利用直接法求距离需找到点在面内的射影,此时常考虑面面垂直的性质定理与几何图形的特殊性质.而间接法中常用的是等积法及转移法.
⑤求角与距离的关键是将空间的角与距离灵活转化为平面上的角与距离,然后将所求量置于一个三角形中,通过解三角形最终求得所需的角与距离
求距离的关键是化归。即空间距离与角向平面距离与角化归,各种具体方法如下:
(1)求空间中两点间的距离,一般转化为解直角三角形或斜三角形。
(2)求点到直线的距离和点到平面的距离,一般转化为求直角三角形斜边上的高;或利用三棱锥的底面与顶点的轮换性转化为三棱锥的高,即用体积法。
空间的角和距离是空间图形中最基本的数量关系,空间的角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解决.
1.空间的角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念,由它们的定义,可得其取值范围,如两异面直线所成的角θ∈(0,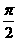 ),直线与平面所成的角θ∈
),直线与平面所成的角θ∈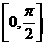 ,二面角的大小,可用它们的平面角来度量,其平面角θ∈(0,π)。
,二面角的大小,可用它们的平面角来度量,其平面角θ∈(0,π)。
对于空间角的计算,总是通过一定的手段将其转化为一个平面内的角,并把它置于一个平面图形,而且是一个三角形的内角来解决,而这种转化就是利用直线与平面的平行与垂直来实现的,因此求这些角的过程也是直线、平面的平行与垂直的重要应用.通过空间角的计算和应用进一步培养运算能力、逻辑推理能力及空间想象能力.
(1)求异面直线所成的角,一般是平移转化法。方法一是在异面直线中的一条直线上选择“特殊点”,作另一条直线的平行线;或过空间任一点分别作两异面直线的平行线,这样就作出了两异面直线所成的角θ,构造一个含θ的三角形,解三角形即可。方法二是补形法:将空间图形补成熟悉的、完整的几何体,这样有利于找到两条异面直线所成的角θ。
(2)求直线与平面所成的角,一般先确定直线与平面的交点(斜足),然后在直线上取一点(除斜足外)作平面的垂线,再连接垂足和斜足(即得直接在平面内的射影),最后解由垂线、斜线、射影所组成的直角三角形,求出直线与平面所成的角
(3)求二面角,一般有直接法和间接法两种。所谓直接法求二面角,就是作出二面角的平面角来解。其中有棱二面角作平面角的方法通常有:①根据定义作二面角的平面角;②垂面法作二面角的平面角;③利用三垂线定理及其逆定理作二面角的平面角;无棱二面角先作出棱后同上进行。间接法主要是投影法:即在一个平面α上的图形面积为S,它在另一个平面β上的投影面积为S′,这两个平面的夹角为θ,则S′=Scosθ。
如求异面直线所成的角常用平移法(转化为相交直线);求直线与平面所成的角常利用射影转化为相交直线所成的角;而求二面角a-l-b的平面角(记作q)通常有以下几种方法:
(1) 根据定义;
(2) 过棱l上任一点O作棱l的垂面g,设g∩a=OA,g∩b=OB,则∠AOB=q(图1);
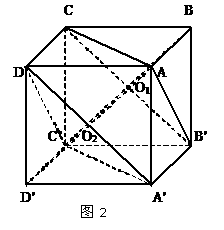
(3) 利用三垂线定理或逆定理,过一个半平面a内一点A,分别作另一个平面b的垂线AB(垂足为B),或棱l的垂线AC(垂足为C),连结AC,则∠ACB=q 或∠ACB=p-q(图2);
(4) 设A为平面a外任一点,AB⊥a,垂足为B,AC⊥b,垂足为C,则∠BAC=q或∠BAC=p-q(图3);
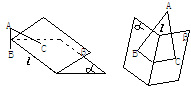 (5) 利用面积射影定理,设平面a内的平面图形F的面积为S,F在平面b内的射影图形的面积为S¢,则cosq=
(5) 利用面积射影定理,设平面a内的平面图形F的面积为S,F在平面b内的射影图形的面积为S¢,则cosq=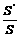 .
.
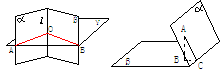
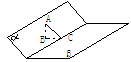
图 1 图 2 图 3
题型1:直线间的距离问题
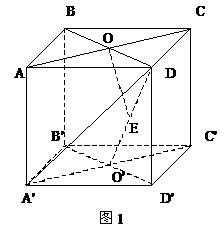 例1.已知正方体
例1.已知正方体 的棱长为1,求直线DA'与AC的距离。
的棱长为1,求直线DA'与AC的距离。
解法1:如图1连结A'C',则AC∥面A'C'D',
连结DA'、DC'、DO',过O作OE⊥DO'于E
因为A'C'⊥面BB'D'D,所以A'C'⊥OE。
又O'D⊥OE,所以OE⊥面A'C'D。
因此OE为直线DA'与AC的距离
在Rt△OO'D中, ,可求得
,可求得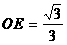
点评:此题是异面直线的距离问题:可作出异面直线的公垂线。
解法2:如图2连接A'C'、DC'、B'C、AB'A',得到分别包含DA'和AC的两个平面A'C'D和平面AB'C,
又因为A'C'∥AC,A'D∥B'C,所以面A'C'D∥面AB'C。
故DA'与AC的距离就是平面A'C'D和平面AB'C的距离,连BD'分别交两平面于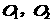 两点,易证
两点,易证 是两平行平面距离
是两平行平面距离
不难算出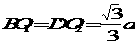 ,所以
,所以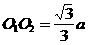 ,所以异面直线BD与
,所以异面直线BD与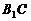 之间的距离为
之间的距离为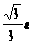 。
。
点评:若考虑到异面直线的公垂线不易做出,可分别过两异面直线作两平面互相平行,则异面直线的距离就是两平面的距离
题型2:线线夹角
例2.如图1,在三棱锥S-ABC中, ,
, ,
,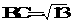 ,
,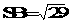 ,求异面直线SC与AB所成角的余弦值。
,求异面直线SC与AB所成角的余弦值。
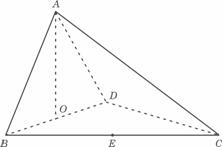
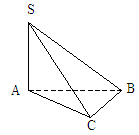
图1
解法1:用公式
当直线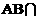 平面
平面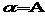 ,AB与
,AB与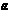 所成的角为
所成的角为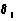 ,l是
,l是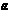 内的一条直线,l与AB在
内的一条直线,l与AB在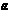 内的射影
内的射影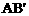 所成的角为
所成的角为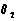 ,则异面直线l与AB所成的角
,则异面直线l与AB所成的角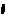 满足
满足 。以此为据求解
。以此为据求解
由题意,知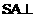 平面ABC,
平面ABC, ,由三垂线定理,知
,由三垂线定理,知 ,所以
,所以 平面SAC。
平面SAC。
因为 ,由勾股定理,得
,由勾股定理,得  。
。
在 中,
中,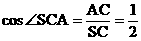 ,在
,在 中,
中,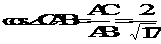 。
。
设SC与AB所成角为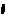 ,则,
,则,
解法2:平移
过点C作CD//BA,过点A作BC的平行线交CD于D,连结SD,则 是异面直线SC与AB所成的角,如图2。又四边形ABCD是平行四边形。
是异面直线SC与AB所成的角,如图2。又四边形ABCD是平行四边形。
由勾股定理,得: 。
。
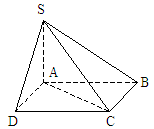
图2
在 中,由余弦定理,得:
中,由余弦定理,得: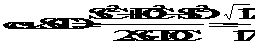 。
。
点评:若不垂直,可经过如下几个步骤求解:(1)恰当选点,作两条异面直线的平行线,构造平面角 ;(2)证明这个角
;(2)证明这个角 (或其补角)就是异面直线所成角;(3)解三角形(常用余弦定理),求出所构造角
(或其补角)就是异面直线所成角;(3)解三角形(常用余弦定理),求出所构造角 的度数
的度数
题型3:点线距离
例3.(2009天津卷理)(本小题满分12分)
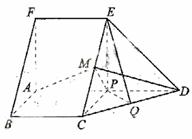
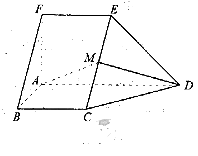 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA 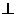 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB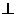 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=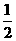 A
A
(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD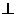 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值
 本小题要考查异面直线所成的角、平面与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想像能力、运算能力和推理论证能力。满分12分.
本小题要考查异面直线所成的角、平面与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想像能力、运算能力和推理论证能力。满分12分.
方法一:(Ⅰ)解:由题设知,BF//CE,所以∠CED(或其补角)为异面直线BF与DE所成的角。设P为AD的中点,连结EP,PC。因为FE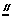 AP,所以FA
AP,所以FA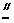 EP,同理AB
EP,同理AB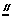 PC。又FA⊥平面ABCD,所以EP⊥平面ABCD。而PC,AD都在平面ABCD内,故EP⊥PC,EP⊥AD。由AB⊥AD,可得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=
PC。又FA⊥平面ABCD,所以EP⊥平面ABCD。而PC,AD都在平面ABCD内,故EP⊥PC,EP⊥AD。由AB⊥AD,可得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=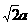 ,故∠CED=60°。所以异面直线BF与DE所成的角的大小为60
,故∠CED=60°。所以异面直线BF与DE所成的角的大小为60
(II)证明:因为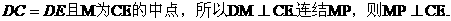
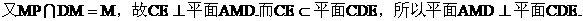 (III)
(III)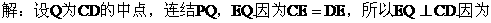
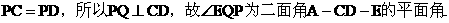
由(I)可得,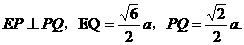
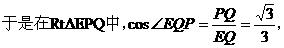
方法二:如图所示,建立空间直角坐标系,
点 为坐标原点。设
为坐标原点。设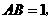 依题意得
依题意得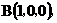
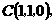
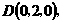
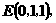
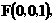
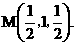
(I)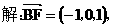
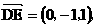
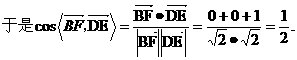
所以异面直线 与
与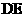 所成的角的大小为
所成的角的大小为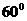 .
.
(II)证明: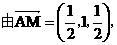
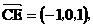
 ,
,
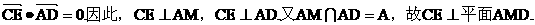
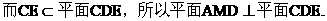
(III)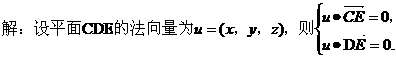
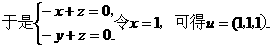
又由题设,平面 的一个法向量为
的一个法向量为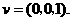
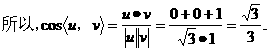
题型4:点面距离
例4.(2009重庆卷理)(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
如题(19)图,在四棱锥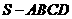 中,
中, 且
且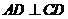 ;平面
;平面
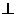 平面
平面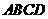 ,
,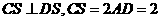 ;
;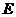 为
为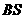 的中点,
的中点,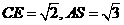 .求:
.求:
(Ⅰ)点 到平面
到平面 的距离;
的距离;
(Ⅱ)二面角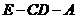 的大小.
的大小.
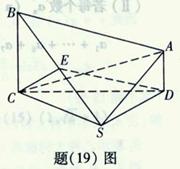
(19)(本小题12分)
解法一:
(Ⅰ)因为AD//BC,且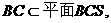 所以
所以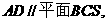 从而A点到平面
从而A点到平面 的距离等于D点到平面
的距离等于D点到平面 的距离。
的距离。
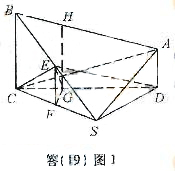 因为平面
因为平面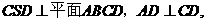 故
故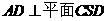 ,从而
,从而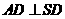 ,由AD//BC,得
,由AD//BC,得
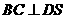 ,又由
,又由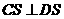 知
知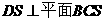 ,从而
,从而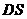 为点A到平面
为点A到平面 的距离,因此在
的距离,因此在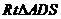 中
中
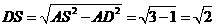
(Ⅱ)如答(19)图1,过E电作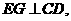 交
交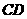 于点G,又过G点作
于点G,又过G点作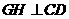 ,交AB于H,故
,交AB于H,故
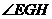 为二面角
为二面角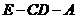 的平面角,记为
的平面角,记为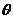 ,过E点作EF//BC,交
,过E点作EF//BC,交 于点F,连结GF,因平面
于点F,连结GF,因平面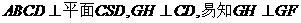 ,故
,故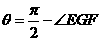 .
.
由于E为BS边中点,故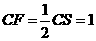 ,在
,在 中,
中,
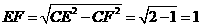 ,因
,因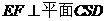 ,又
,又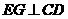
故由三垂线定理的逆定理得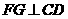 ,从而又可得
,从而又可得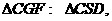
因此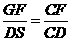 而在
而在 中,
中,
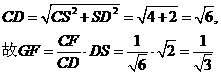
在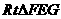 中,
中,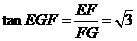 可得
可得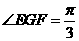 ,故所求二面角的大小为
,故所求二面角的大小为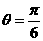
解法二:
(Ⅰ)如答(19)图2,以S(O)为坐标原点,射线OD,OC分别为x轴,y轴正向,建立空间坐标系,设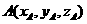 ,因平面
,因平面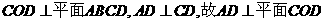
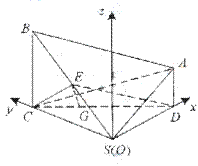 即点A在xoz平面上,因此
即点A在xoz平面上,因此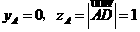
又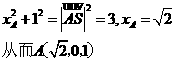
因AD//BC,故BC⊥平面CSD,即BCS与平面
yOx重合,从而点A到平面BCS的距离为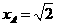 .
.
(Ⅱ)易知C(0,2,0),D(,0,0). 因E为BS的中点.
ΔBCS为直角三角形 ,
知 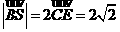
设B(0,2, 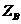 ),
),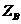 >0,则
>0,则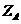 =2,故B(0,2,2),所以E(0,1,1) .
=2,故B(0,2,2),所以E(0,1,1) .
在CD上取点G,设G(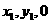 ),使GE⊥CD
),使GE⊥CD
由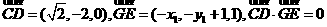 故
故
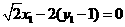 ①
①
又点G在直线CD上,即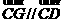 ,由
,由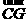 =(
=(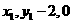 ),则有
),则有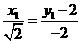 ②
②
联立①、②,解得G=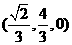 ,
,
故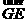 =
=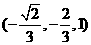 .又由AD⊥CD,所以二面角E-CD-A的平面角为向量
.又由AD⊥CD,所以二面角E-CD-A的平面角为向量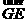 与向量
与向量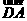 所成的角,记此角为
所成的角,记此角为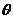 .
.
因为 =
=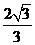 ,
,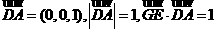 ,所
,所
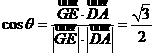
故所求的二面角的大小为 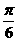 .
.
点评:本小题主要考查直线与平面的位置关系、异面直线所成的角以及点到平面的距离等基本知识,考查空间想象能力、逻辑思维能力和运算能力
题型5:线面距离
例5.(2009重庆卷文)(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
如题(18)图,在五面体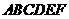 中,
中,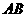 ∥
∥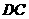 ,
,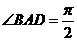 ,
,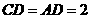 ,四边形
,四边形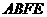 为平行四边形,
为平行四边形,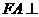 平面
平面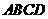 ,
,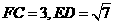 .求:
.求:
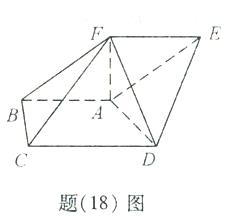 (Ⅰ)直线
(Ⅰ)直线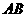 到平面
到平面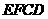 的距离;
的距离;
(Ⅱ)二面角 的平面角的正切值.
的平面角的正切值.
解法一:
(Ⅰ)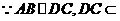 平面
平面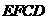 ,
,  AB到面
AB到面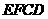 的距离等于点A到面
的距离等于点A到面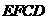 的距离,过点A作
的距离,过点A作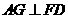 于G,因
于G,因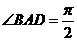
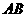 ∥
∥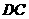 ,故
,故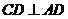 ;又
;又
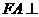 平面
平面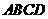 ,由三垂线定理可知,
,由三垂线定理可知,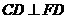 ,故
,故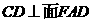 ,知
,知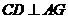 ,所以AG为所求直线AB到面
,所以AG为所求直线AB到面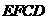 的距离
的距离
在 中,
中,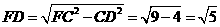
由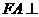 平面
平面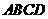 ,得
,得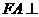 AD,从而在
AD,从而在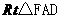 中,
中,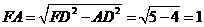

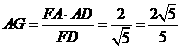 。即直线
。即直线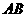 到平面
到平面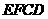 的距离为
的距离为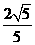 。
。
(Ⅱ)由己知,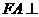 平面
平面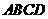 ,得
,得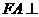 AD,又由
AD,又由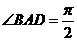 ,知
,知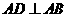 ,故
,故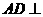 平面ABFE
平面ABFE

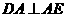 ,所以,
,所以, 为二面角
为二面角 的平面角,记为
的平面角,记为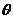 .
.
在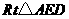 中,
中, 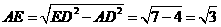 ,由
,由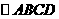 得,
得,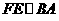 ,从而
,从而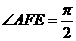
在 中,
中, 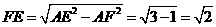 ,故
,故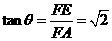
 所以二面角
所以二面角 的平面角的正切值为
的平面角的正切值为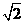 .
.
解法二:
(Ⅰ)如图以A点为坐标原点,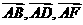 的方向为
的方向为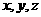 的正方向建立空间直角坐标系数,则
的正方向建立空间直角坐标系数,则
A(0,0,0) C(2,2,0) D(0,2,0) 设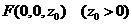 可得
可得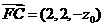 ,由
,由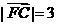 .即
.即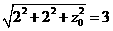 ,解得
,解得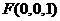

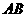 ∥
∥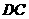 ,
,
 面
面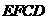 ,所以直线AB到面
,所以直线AB到面 的距离等于点A到面
的距离等于点A到面 的距离。设A点在平面
的距离。设A点在平面 上的射影点为
上的射影点为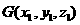 ,则
,则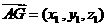 因
因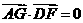 且
且 ,而
,而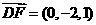
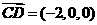 ,此即
,此即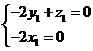 解得
解得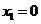 ① ,知G点在
① ,知G点在 面上,故G点在FD上.
面上,故G点在FD上.
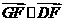 ,
,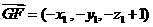 故有
故有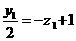 ② 联立①,②解得,
② 联立①,②解得, 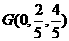

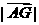 为直线AB到面
为直线AB到面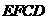 的距离. 而
的距离. 而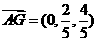 所以
所以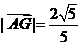
(Ⅱ)因四边形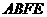 为平行四边形,则可设
为平行四边形,则可设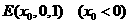 ,
,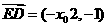 .由
.由
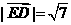 得
得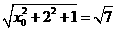 ,解得
,解得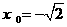 .即
.即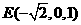 .故
.故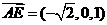
由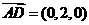 ,
,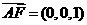 因
因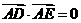 ,
,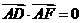 ,故
,故 为二面角
为二面角 的平面角,又
的平面角,又
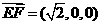 ,
,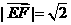 ,
,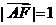 ,所以
,所以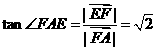
点评:线面距离往往转化成点面距离来处理,最后可能转化为空间几何体的体积求得,体积法不用得到垂线。
题型6:线面夹角
 例6.2009湖南卷文)(本小题满分12分)
例6.2009湖南卷文)(本小题满分12分)
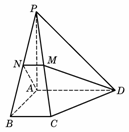
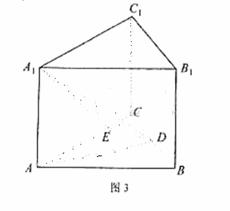 如图3,在正三棱柱
如图3,在正三棱柱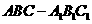 中,AB=4,
中,AB=4, 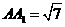 ,点D是BC的中点,点E在AC上,且DE
,点D是BC的中点,点E在AC上,且DE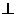
 E.
E.
(Ⅰ)证明:平面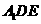
 平面
平面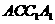
(Ⅱ)求直线AD和平面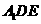 所成角的正弦值
所成角的正弦值
解:(Ⅰ)如图所示,由正三棱柱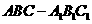 的性质知
的性质知
 平面
平面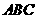 .
.
又DE 平面ABC,所以DE
平面ABC,所以DE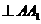 .而DE
.而DE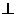
 E,
E,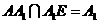 ,
,
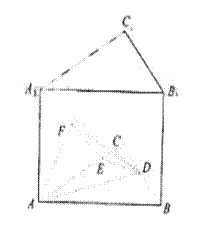 所以DE⊥平面
所以DE⊥平面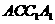 .又DE
.又DE 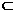 平面
平面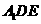 ,
,
故平面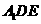 ⊥平面
⊥平面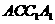 .
.
(Ⅱ)解法 1: 过点A作AF垂直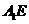 于点
于点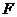 ,
,
连接DF.由(Ⅰ)知,平面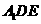 ⊥平面
⊥平面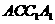 ,
,
所以AF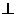 平面
平面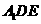 ,故
,故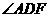 是直线AD和
是直线AD和
平面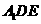 所成的角。 因为DE
所成的角。 因为DE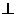
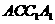 ,
,
所以DE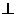 AC.而
AC.而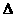 ABC是边长为4的正三角形,
ABC是边长为4的正三角形,
于是AD=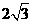 ,AE=4-CE=4-
,AE=4-CE=4-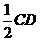 =3.
=3.
又因为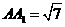 ,所以
,所以 E=
E= 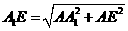
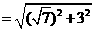 =
4,
=
4,
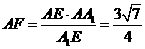 ,
, 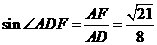 .
.
即直线AD和平面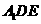 所成角的正弦值为
所成角的正弦值为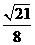
解法2 : 如图所示,设O是AC的中点,以O为原点建立空间直角坐标系,
则相关各点的坐标分别是A(2,0,0,),  (2,0,
(2,0,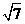 ),
D(-1,
),
D(-1, 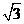 ,0), E(-1,0,0).
,0), E(-1,0,0).
易知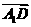 =(-3,
=(-3,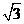 ,-
,-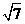 ),
),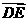 =(0,-
=(0,-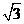 ,0),
,0),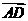 =(-3,
=(-3,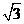 ,0).
,0).
设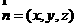 是平面
是平面 的一个法向量,则
的一个法向量,则
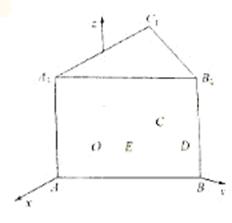
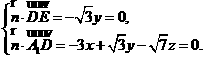
解得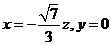 .
.
故可取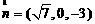 .于
.于
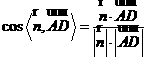 =
=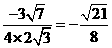
由此即知,直线AD和平面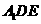 所成角的正弦值为
所成角的正弦值为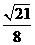
点评:本题主要考查几何体的概念、线面夹角、两平面垂直等。能力方面主要考查空间想象能力、逻辑思维能力和运算能力
题型7:面面距离
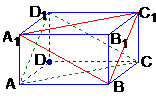 例7.在长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,如图:
例7.在长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1=2,如图:
(1)求证:平面A1BC1∥平面ACD1;
(2)求(1)中两个平行平面间的距离;
(3)求点B1到平面A1BC1的距离。
(1)证明:由于BC1∥AD1,则BC1∥平面ACD1,
同理,A1B∥平面ACD1,则平面A1BC1∥平面ACD1。
(2)解:设两平行平面A1BC1与ACD1间的距离为d,则d等于D1到平面A1BC1的距离。易求A1C1=5,A1B=2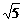 ,BC1=
,BC1=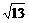 ,则cosA1BC1=
,则cosA1BC1=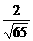 ,则sinA1BC1=
,则sinA1BC1=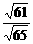 ,则S
,则S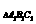 =
=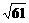 。
。
由于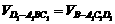 ,则
,则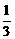 S
S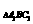 ·d=
·d=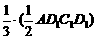 ·BB1,代入求得d=
·BB1,代入求得d=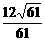 ,即两平行平面间的距离为
,即两平行平面间的距离为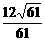 。
。
(3)解:由于线段B1D1被平面A1BC1所平分,则B1、D1到平面A1BC1的距离相等,则由(2)知点B1到平面A1BC1的距离等于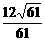 。
。
点评:立体几何图形必须借助面的衬托,点、线、面的位置关系才能显露地“立”起来。在具体的问题中,证明和计算经常依附于某种特殊的辅助平面即基面。这个辅助平面的获取正是解题的关键所在,通过对这个平面的截得,延展或构造,纲举目张,问题就迎刃而解了。
 题型8:面面角
题型8:面面角
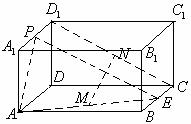
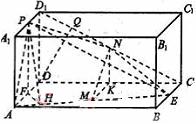
例8.如图,在长方体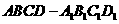 中,
中,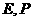 分别是
分别是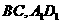 的中点,
的中点,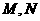 分别是
分别是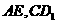 的中点,
的中点,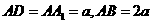 。
。
(Ⅰ)求证: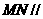 面
面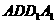 ;
;
(Ⅱ)求二面角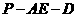 的大小。
的大小。
 (Ⅲ)求三棱锥
(Ⅲ)求三棱锥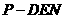 的体积。
的体积。
解析:(Ⅰ)证明:取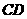 的中点
的中点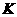 ,连结
,连结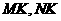
∵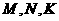 分别为
分别为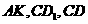 的中点,
的中点,
∵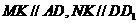 ,∴
,∴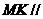 面
面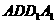 ,
,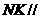 面
面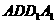
∴面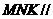 面
面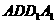 ∴
∴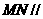 面
面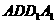
(Ⅱ)设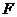 为
为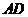 的中点
的中点
∵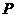 为
为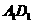 的中点 ∴
的中点 ∴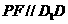 ∴
∴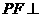 面
面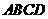
作 ,交
,交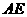 于
于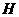 ,连结
,连结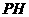 ,则由三垂线定理得
,则由三垂线定理得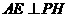 。
。
从而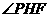 为二面角
为二面角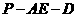 的平面角
的平面角
在 中,
中,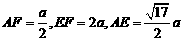 ,从而
,从而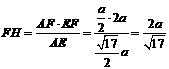 。
。
在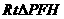 中,
中, ,故二面角
,故二面角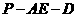 的正切值为
的正切值为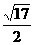 。
。
(Ⅲ)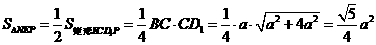 ,
,
作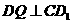 ,交
,交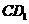 于
于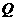 ,由
,由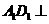 面
面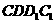 得
得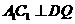 ,
,
∴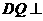 面
面 ,
,
∴在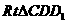 中,
中,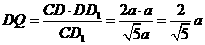 ,
,
∴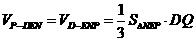
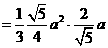
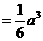 。
。
点评:求角和距离的基本步骤是作、证、算。此外还要特别注意融合在运算中的推理过程,推理是运算的基础,运算只是推理过程的延续。如求二面角,只有根据推理过程找到二面角后,进行简单的运算,才能求出。因此,求角与距离的关键还是直线与平面的位置关系的论证。
3.等角定理
如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等。
推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等。
2. 夹角
夹角
空间中的各种角包括异面直线所成的角,直线与平面所成的角和二面角,要理解各种角的概念定义和取值范围,其范围依次为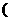 0°,90°
0°,90°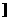 、[0°,90°]和[0°,180°]。
、[0°,90°]和[0°,180°]。
(1)两条异面直线所成的角
求法:1先通过其中一条直线或者两条直线的平移,找出这两条异面直线所成的角,然后通过解三角形去求得;2通过两条异面直线的方向量所成的角来求得,但是注意到异面直线所成角得范围是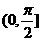 ,向量所成的角范围是
,向量所成的角范围是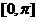 ,如果求出的是钝角,要注意转化成相应的锐角
,如果求出的是钝角,要注意转化成相应的锐角
(2)直线和平面所成的角
求法:“一找二证三求”,三步都必须要清楚地写出来。除特殊位置外,主要是指平面的斜线与平面所成的角,根据定义采用“射影转化法”
(3)二面角的度量是通过其平面角来实现的
解决二面角的问题往往是从作出其平面角的图形入手,所以作二面角的平面角就成为解题的关键。通常的作法有:(Ⅰ)定义法;(Ⅱ)利用三垂线定理或逆定理;(Ⅲ)自空间一点作棱垂直的垂面,截二面角得两条射线所成的角,俗称垂面法.此外,当作二面角的平面角有困难时,可用射影面积法解之,cos =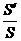 ,其中S 为斜面面积,S′为射影面积, 为斜面与射影面所成的二面角
,其中S 为斜面面积,S′为射影面积, 为斜面与射影面所成的二面角
1.距离
空间中的距离是立体几何的重要内容,其内容主要包括:点点距,点线距,点面距,线线距,线面距,面面距。其中重点是点点距、点线距、点面距以及两异面直线间的距离.因此,掌握点、线、面之间距离的概念,理解距离的垂直性和最近性,理解距离都指相应线段的长度,懂得几种距离之间的转化关系,所有这些都是十分重要的
求距离的重点在点到平面的距离,直线到平面的距离和两个平面的距离可以转化成点到平面的距离,一个点到平面的距离也可以转化成另外一个点到这个平面的距离。
(1)两条异面直线的距离
两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离;求法:如果知道两条异面直线的公垂线,那么就转化成求公垂线段的长度
(2)点到平面的距离
平面外一点P 在该平面上的射影为P′,则线段PP′的长度就是点到平面的距离;求法:1“一找二证三求”,三步都必须要清楚地写出来。2等体积法。
(3)直线与平面的距离:一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离;
(4)平行平面间的距离:两个平行平面的公垂线段的长度,叫做两个平行平面的距离。
求距离的一般方法和步骤:应用各种距离之间的转化关系和“平行移动”的思想方法,把所求的距离转化为点点距、点线距或点面距求之,其一般步骤是:①找出或作出表示有关距离的线段;②证明它符合定义;③归到解某个三角形.若表示距离的线段不容易找出或作出,可用体积等积法计算求之。异面直线上两点间距离公式,如果两条异面直线a 、b 所成的角为 ,它们的公垂线AA′的长度为d ,在a 上有线段A′E =m ,b 上有线段AF =n ,那么EF =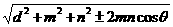 (“±”符号由实际情况选定)
(“±”符号由实际情况选定)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com