
题目列表(包括答案和解析)
4. 7月份,有一款新服装投入某市场销售,7月1日该款服装仅销售出3件,7月2日售出6件,7月3日售出9件,7月4日售出12件,尔后,每天售出的件数分别递增3件直到日销售量达到最大(只有1天)后,每天销售的件数开始下降,分别递减2件,到7月31日刚好售出3件。
(1)问7月几号该款服装销售件数最多?其最大值是多少?
(2)按规律,当该商场销售此服装达到200件时,社会上就开始流行,而日销售量连续下降并低于20件时,则不再流行,问该款服装在社会上流行几天?说明理由。
20、(文)某地区预计明年从年初开始的前x个月内,对某种商品的需求总量f(x)(万件)与月份x的近似关系为: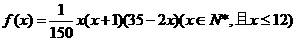
(1)写出明年第x个月的需求量g(x)(万件)与月份x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(2)如果将该商品每月都投放市场P万件(销售未完的商品都可以在以后各月销售),要保证每月都足量供应,问P至少为多少万件?
3. (理)某城市2004年末粮食储备量为100万吨,预计此后每年耗用上一年末粮食储备量的5%,并且每年新增粮食x万吨。
(1)记2004年末的粮食储备量为a1万吨,此后各年末的粮食储备量为a2万吨,a3万吨,……,写出a1,a2,a3和an(n∈N*)的表示式;
(2)受条件限制,该城市的粮食储备量不能超过150万吨,那么每年新增粮食储备量不应超过多少万吨?
2. 商学院为推进后勤社会化改革,与桃园新区商定:由该区向建设银行贷款500万元在桃园新区为学院建一栋可容纳一千人的学生公寓,工程于2002年初动工,年底竣工并交付使用,公寓管理处采用收费还贷偿还建行贷款(年利率5%,按复利计算),公寓所收费用除去物业管理费和水电费18万元.其余部分全部在年底还建行贷款.
商学院为推进后勤社会化改革,与桃园新区商定:由该区向建设银行贷款500万元在桃园新区为学院建一栋可容纳一千人的学生公寓,工程于2002年初动工,年底竣工并交付使用,公寓管理处采用收费还贷偿还建行贷款(年利率5%,按复利计算),公寓所收费用除去物业管理费和水电费18万元.其余部分全部在年底还建行贷款.
(1)若公寓收费标准定为每生每年800元,问到哪一年可偿还建行全部贷款;
(2)若公寓管理处要在2010年底把贷款全部还清,则每生每年的最低收费标准是多少元(精确到元).(参考数据:lg1.7343=0.2391,lgl.05=0.0212,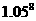 =1.4774)
=1.4774)
1.某种商品每件进价12元,售价20元,每天可卖出48件。若售价降低,销售量可以增加,且售价降低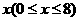 元时,每天多卖出的件数与
元时,每天多卖出的件数与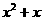 成正比。已知商品售价降低3元时,一天可多卖出36件。
成正比。已知商品售价降低3元时,一天可多卖出36件。
(1)试将该商品一天的销售利润表示成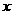 的函数;
的函数;
(2)该商品售价为多少元时一天的销售利润最大?
7.如图,在四棱锥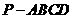 中,底面
中,底面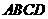 为矩形,
为矩形,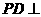 底面
底面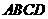 ,
,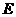 是
是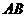 上
上
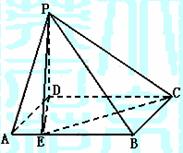 一点,
一点,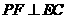 . 已知
. 已知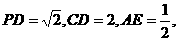
求(Ⅰ)异面直线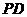 与
与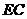 的距离;
的距离;
(Ⅱ)二面角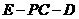 的大小.
的大小.
解:(Ⅰ)以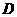 为原点,
为原点,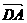 、
、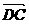 、
、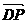 分别为
分别为
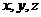 轴建立空间直角坐标系.
轴建立空间直角坐标系.
由已知可得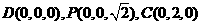
设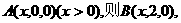
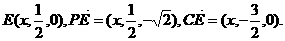 由
由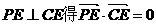 ,
,
即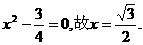 由
由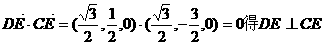 ,
,
又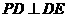 ,故
,故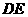 是异面直线
是异面直线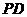 与
与 的公垂线,易得
的公垂线,易得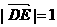 ,故异面直线
,故异面直线
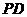 ,
, 的距离为
的距离为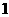 .
.
(Ⅱ)作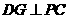 ,可设
,可设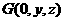 .由
.由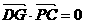 得
得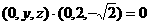
即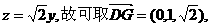 作
作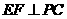 于
于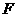 ,设
,设 ,
,
则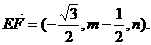
由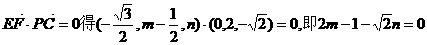 ,
,
又由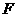 在
在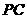 上得
上得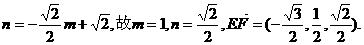
因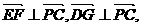 故
故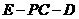 的平面角
的平面角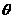 的大小为向量
的大小为向量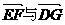 的夹角.
的夹角.
故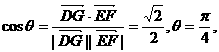 即二面角
即二面角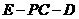 的大小为
的大小为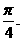
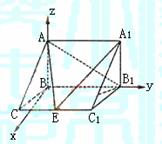
6.如图,在三棱柱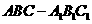 中,
中,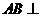 侧面
侧面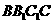 ,
,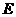 为棱
为棱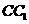 上异于
上异于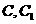 的一点,
的一点,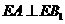 ,已知
,已知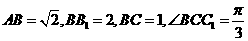 ,求:
,求:
(Ⅰ)异面直线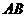 与
与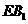 的距离;
的距离;
(Ⅱ)二面角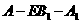 的平面角的正切值.
的平面角的正切值.
解:(I)以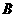 为原点,
为原点,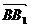 、
、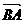 分别为
分别为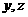 轴建立空间直角坐标系.
轴建立空间直角坐标系.
 由于,
由于,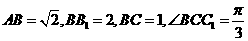
在三棱柱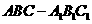 中有
中有
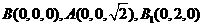 ,
,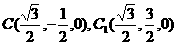
设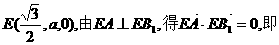
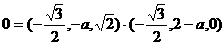
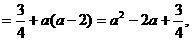
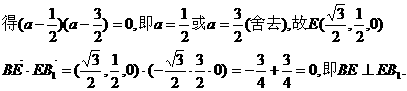
又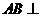 侧面
侧面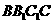 ,故
,故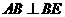 . 因此
. 因此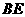 是异面直线
是异面直线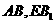 的公垂线,
的公垂线,
则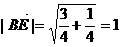 ,故异面直线
,故异面直线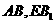 的距离为
的距离为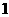 .
.
(II)由已知有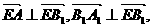 故二面角
故二面角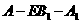 的平面角
的平面角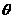 的大小为向量
的大小为向量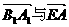 的夹角.
的夹角.
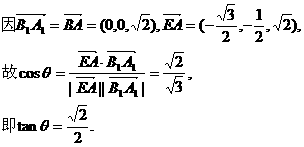
5.如图,在长方体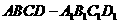 ,中,
,中,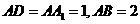 ,点
,点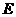 在棱
在棱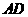 上移动.(1)证明:
上移动.(1)证明: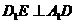 ;
;
(2)当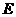 为
为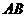 的中点时,求点
的中点时,求点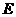 到面
到面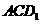 的距离;
的距离;
(3)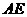 等于何值时,二面角
等于何值时,二面角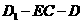 的大小为
的大小为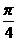 .
.
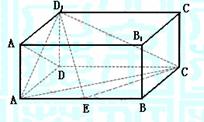
解:以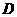 为坐标原点,直线
为坐标原点,直线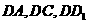 分别为
分别为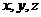 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设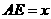 ,则
,则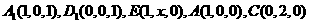
(1)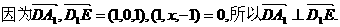
(2)因为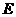 为
为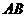 的中点,则
的中点,则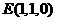 ,从而
,从而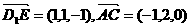 ,
,
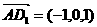 ,设平面
,设平面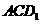 的法向量为
的法向量为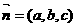 ,则
,则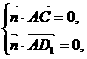
也即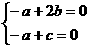 ,得
,得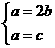 ,从而
,从而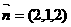 ,所以点
,所以点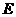 到平面
到平面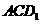 的距离为
的距离为
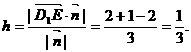
(3)设平面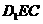 的法向量
的法向量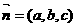 ,∴
,∴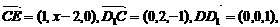
由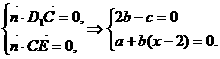 令
令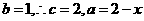 ,
,
∴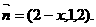
依题意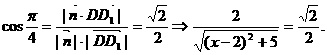
∴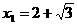 (不合,舍去),
(不合,舍去),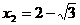 .
.
∴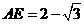 时,二面角
时,二面角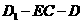 的大小为
的大小为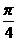 .
.
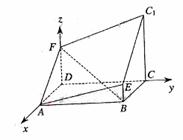
4.如图所示的多面体是由底面为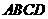 的长方体被截面
的长方体被截面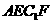 所截面而得到的,其中
所截面而得到的,其中
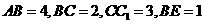 .
.
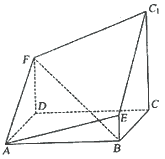 (Ⅰ)求
(Ⅰ)求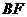 的长;
的长;
(Ⅱ)求点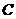 到平面
到平面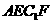 的距离.
的距离.
解:(I)建立如图所示的空间直角坐标系,则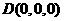 ,
,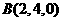
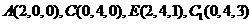 设
设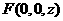 .
.
 ∵
∵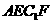 为平行四边形,
为平行四边形,

(II)设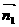 为平面
为平面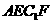 的法向量,
的法向量,
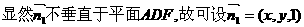
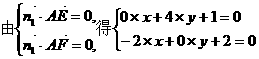
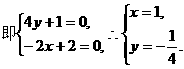
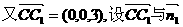 的夹角为
的夹角为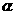 ,则
,则
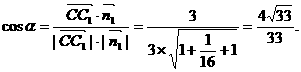
∴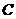 到平面
到平面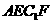 的距离为
的距离为
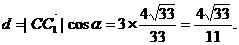
3.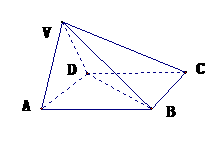 如图,在四棱锥
如图,在四棱锥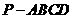 中,底面
中,底面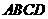 为矩形,
为矩形,
侧棱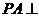 底面
底面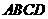 ,
,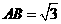 ,
,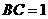 ,
,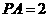 ,
,
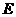 为
为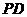 的中点.
的中点.
(Ⅰ)求直线 与
与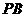 所成角的余弦值;
所成角的余弦值;
(Ⅱ)在侧面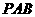 内找一点
内找一点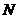 ,使
,使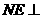 面
面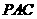 ,
,
并求出点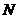 到
到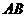 和
和 的距离.
的距离.
解:(Ⅰ)建立如图所示的空间直角坐标系,
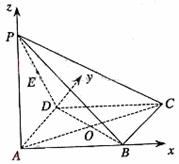 则
则 的坐标为
的坐标为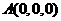 、
、
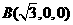 、
、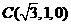 、
、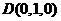 、
、
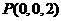 、
、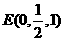 ,
,
从而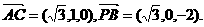
设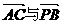 的夹角为
的夹角为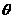 ,则
,则
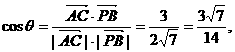
∴ 与
与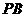 所成角的余弦值为
所成角的余弦值为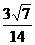 .
.
(Ⅱ)由于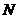 点在侧面
点在侧面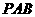 内,故可设
内,故可设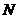 点坐标为
点坐标为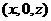 ,则
,则
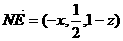 ,由
,由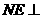 面
面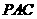 可得,
可得,
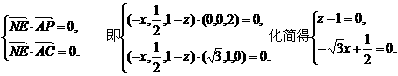 ∴
∴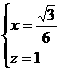
即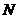 点的坐标为
点的坐标为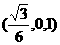 ,从而
,从而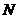 点到
点到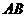 和
和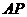 的距离分别为
的距离分别为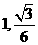 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com