
题目列表(包括答案和解析)
4.计算矩阵的乘积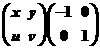 =______________ .
=______________ .
3.线性方程组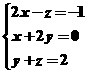 的增广矩阵是__________________.
的增广矩阵是__________________.
2.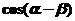 计算公式可用行列式表示为_____________.
计算公式可用行列式表示为_____________.
1.规定矩阵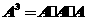 ,若矩阵
,若矩阵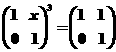 ,则
,则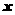 的值是_____________.
的值是_____________.
2.直角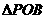 中,
中,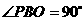 ,以
,以 为圆心、
为圆心、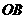 为半径作圆弧交
为半径作圆弧交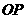 于
于 点.若弧AB等分△POB的面积,且∠AOB=
点.若弧AB等分△POB的面积,且∠AOB=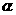 弧度,则( )
弧度,则( )
A.tan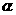 =
=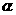 B.tan
B.tan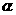 =2
=2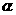
C.sin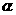 =2cos
=2cos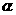 D.2 sin
D.2 sin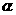 = cos
= cos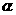
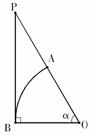
1.用数学归纳法证明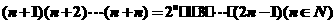 ,从“
,从“ 到
到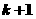 ”左端需增的代数式为
( )
”左端需增的代数式为
( )
 A.
A. 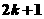 B.
B. 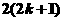 C.
C. 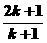 D.
D. 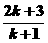
4.(本小题满分17分)
 某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
|
项 目 类 别 |
年固定 成本 |
每件产品 成本 |
每件产品 销售价 |
每年最多可 生产的件数 |
|
A产品 |
20 |
m |
10 |
200 |
|
B产品 |
40 |
8 |
18 |
120 |
其中年固定成本与年生产的件数无关,m为待定常数,其值由生产A产品的原材料价格决定,预计 .另外,年销售
.另外,年销售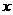 件B产品时需上交
件B产品时需上交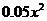 万美元的特别关税.假设生产出来的产品都能在当年销售出去.
万美元的特别关税.假设生产出来的产品都能在当年销售出去.
(Ⅰ)写出该厂分别投资生产A、B两种产品的年利润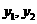 与生产相应产品的件数
与生产相应产品的件数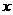 之间的函数关系并指明其定义域;
之间的函数关系并指明其定义域;
(Ⅱ)如何投资才可获得最大年利润?请你做出规划.
3.(本题满分18分)第1小题4分,第2小题4分,第3小题4分,第4小题6分.
在统计学中,我们学习过方差的概念,其计算公式为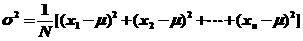 ,并且知道,其中
,并且知道,其中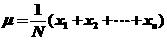 为
为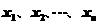 的平均值.
的平均值.
类似地,现定义“绝对差”的概念如下:设有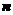 个实数
个实数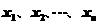 ,称函数
,称函数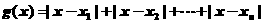 为此
为此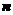 个实数的绝对差.
个实数的绝对差.
(1)设有函数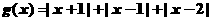 ,试问当
,试问当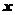 为何值时,函数
为何值时,函数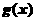 取到最小值,并求最小值;
取到最小值,并求最小值;
(2)设有函数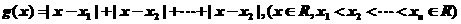 ,
,
试问:当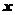 为何值时,函数
为何值时,函数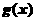 取到最小值,并求最小值;
取到最小值,并求最小值;
(3)若对各项绝对值前的系数进行变化,试求函数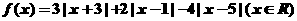 的最值;
的最值;
(4)受(3)的启发,试对(2)作一个推广,给出“加权绝对差”的定义,并讨论该函数的最值(写出结果即可).
2.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知函数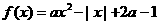 (
(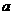 为实常数).
为实常数).
(1)若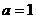 ,作函数
,作函数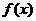 的图像;
的图像;
(2)设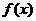 在区间
在区间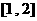 上的最小值为
上的最小值为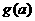 ,求
,求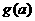 的表达式;
的表达式;
(3)设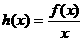 ,若函数
,若函数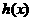 在区间
在区间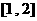 上是增函数,求实数
上是增函数,求实数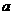 的取值范围.
的取值范围.
1.(本题满分15分)第1小题满分4分,第2小题满分11分
设函数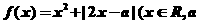 为实数).
为实数).
(1)若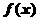 为偶函数,求实数
为偶函数,求实数 的值;
(2)设
的值;
(2)设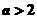 ,求函数
,求函数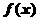 的最小值.
的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com