
题目列表(包括答案和解析)
3.学好几何概率对于解决后续均匀分布的问题有很大帮助。
2.有关几何概率的题目难度不大,但需要准确理解题意,利用图形分析问题。本讲将着重介绍如何利用图形解决几何概率的相关问题;
1.几何概率是考研大纲上要求的基本内容,也是近年来新增考察内容之一;
题型1:线长问题
例1.
(09山东11)在区间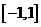 上随机取一个数
上随机取一个数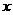 ,
,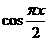 的值介于0到
的值介于0到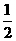 之间的概率
之间的概率
为 ( )
A.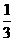 B.
B.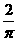 C.
C. 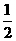 D.
D.
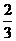
[解析]在区间[-1,1]上随机取一个数x,即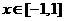 时,要使
时,要使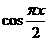 的值介于0到
的值介于0到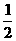 之间,需使
之间,需使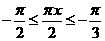 或
或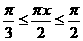 ∴
∴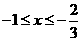 或
或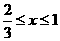 ,区间长度为
,区间长度为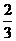 ,由几何概型知
,由几何概型知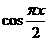 的值介于0到
的值介于0到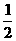 之间的概率为
之间的概率为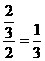 .故选A.
.故选A.
答案 A
例2.(2009辽宁卷文)ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为 ( )
A.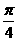 B.
B.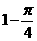 C.
C.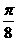 D.
D.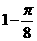
[解析]长方形面积为2,以O为圆心,1为半径作圆,在矩形内部的部分(半圆)面积为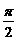
因此取到的点到O的距离小于1的概率为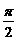 ÷2=
÷2=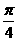
取到的点到O的距离大于1的概率为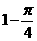
答案 B
 例3.假设车站每隔 10 分钟发一班车,随机到达车站,问等车时间不超过 3
分钟的概率 ?
例3.假设车站每隔 10 分钟发一班车,随机到达车站,问等车时间不超过 3
分钟的概率 ?
解:以两班车出发间隔 ( 0,10 ) 区间作为样本空间 S,乘客随机地到达,即在这个长度是 10 的区间里任何一个点都是等可能地发生,因此是几何概率问题。
要使得等车的时间不超过 3 分钟,即到达的时刻应该是图中 A 包含的样本点,
p= =
=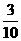 = 0.3 。
= 0.3 。
题型2:面积问题
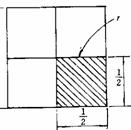 例4.投镖游戏中的靶子由边长为1米的四方板构成,并将此板分成四个边长为1/2米的小方块。实验是向板中投镖,事件A表示投中阴影部分为成功,考虑事件A发生的概率。
例4.投镖游戏中的靶子由边长为1米的四方板构成,并将此板分成四个边长为1/2米的小方块。实验是向板中投镖,事件A表示投中阴影部分为成功,考虑事件A发生的概率。
分析与解答:类似于引例1的解释,完全可以把此引例中的实验所对应的基本事件组与大的正方形区域联系在一起,既事件组中的每一个基本事件与大正方形区域中的每一个点一一对应,则事件A所包含的基本事件就与阴影正方形中的点一一对应,这样我们用阴影正方形的面积除以大正方形的面积表示事件A的概率是合理的。这一点我们完全可以用引例1的方法验证其正确性
解析:P(A)=(1/2)2/12=1/4。
例5.(CB对讲机问题)(CB即CitizenBand市民波段的英文缩写)两个CB对讲机持有者,莉莉和霍伊都为卡尔货运公司工作,他们的对讲机的接收范围为25公里,在下午3:0O时莉莉正在基地正东距基地30公里以内的某处向基地行驶,而霍伊在下午3:00时正在基地正北距基地40公里以内的某地向基地行驶,试问在下午3:0O时他们能够通过对讲机交谈的概率有多大?
解:设x和y分别代表莉莉和霍伊距某地的距离,
于是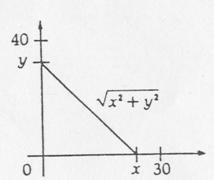
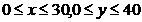
则他俩所有可能的距离的数据构成有序点对(x,y),这里x,y都在它们各自的限制范围内,则所有这样的有序数对构成的集合即为基本事件组对应的几何区域,每一个几何区域中的点都代表莉莉和霍伊的一个特定的位置, 他们可以通过对讲机交谈的事件仅当他们之间的距离不超过25公里时发生(如右图)因此构成该事件的点由满足不等式
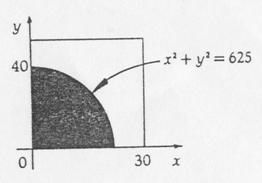
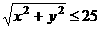
的数对组成,此不等式等价于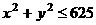
右图中的方形区域代表基本事件组,阴影部分代表所求事件,方形区域的面积为1200平方米公里,而事件的面积为
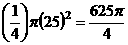 ,
,
于是有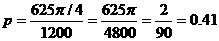 。
。
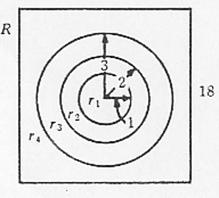
例6.(意大利馅饼问题)山姆的意大利馅饼屋中设有一个投镖靶 该靶为正方形板.边长为18厘米,挂于前门附近的墙上,顾客花两角伍分的硬币便可投一镖并可有机会赢得一种意大利馅饼中的一个,投镖靶中画有三个同心圆,圆心在靶的中心,当投镖击中半径为1厘米的最内层圆域时.可得到一个大馅饼;当击中半径为1厘米到2厘米之间的环域时,可得到一个中馅饼;如果击中半径为2厘米到3厘米之间的环域时,可得到一个小馅饼,如果击中靶上的其他部分,则得不到谄饼,我们假设每一个顾客都能投镖中靶,并假设每个圆的周边线没有宽度,即每个投镖不会击中线上,试求一顾客将嬴得:
(a)一张大馅饼,
(b)一张中馅饼,
(c)一张小馅饼,
(d)没得到馅饼的概率
解析:我们实验的样本空间可由一个边长为18的正方形表示。右图表明R和子区域r1、r2、r3和r,它们分别表示得大馅饼、中馅饼、小馅饼或没得到馅饼的事件
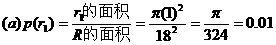 ;
;
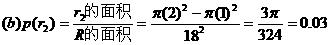 ;
;
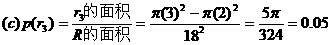 ;
;
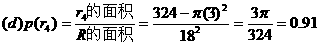 。
。
题型3:体积问题
例7.(1)在400毫升自来水中有一个大肠杆菌,今从中随机取出2毫升水样放到显微镜下观察,求发现大肠杆菌的概率。
解析:由于取水样的随机性,所求事件的概率等于水样的体积与总体积之比,即2/400=0.005。
(2)如果在一个5万平方公里的海域里有表面积达40平方公里的大陆架贮藏着石油,假如在这海领域里随意选定一点钻探,问钻到石油的概率是多少?
解析:由于选点的随机性,可以认为该海域中各点被选中的可能性是一样的,因而所求概率自然认为等于贮油海域的面积与整个海域面积之比,即等于40/50000=0.0008。
例8.在线段[0,1]上任意投三个点,问由0至三点的三线段,能构成三角形与不能构成三角形这两个事件中哪一个事件的概率大。
解析:设0到三点的三线段长分别为x,y,z,即相应的 z
右端点坐标为x,y,z,显然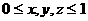 。这三条线
1
C
。这三条线
1
C
段构成三角形的充要条件是: A D
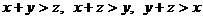 。
。
在线段[0,1]上任意投三点x,y,z。与立方体
0 1 y
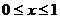 ,
,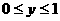 ,
,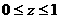 中的点
中的点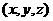 1
1
一一对应,可见所求“构成三角形”的概率,等价于x B
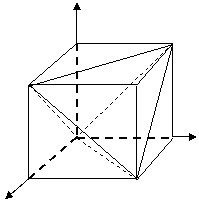 边长为1的立方体T中均匀地掷点,而点落在
边长为1的立方体T中均匀地掷点,而点落在
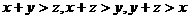 区域中的概率;这也就是落在图中由ΔADC,ΔADB,ΔBDC,ΔAOC,ΔAOB,ΔBOC所围成的区域G中的概率。由于
区域中的概率;这也就是落在图中由ΔADC,ΔADB,ΔBDC,ΔAOC,ΔAOB,ΔBOC所围成的区域G中的概率。由于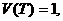
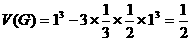 ,
,
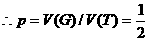
由此得,能与不能构成三角形两事件的概率一样大。
题型4:随机模拟
例9.随机地向半圆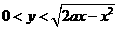 (
(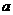 为正常数)内掷一点,点落在园内任何区域的概率与区域的面积成正比,求原点与该点的连线与
为正常数)内掷一点,点落在园内任何区域的概率与区域的面积成正比,求原点与该点的连线与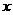 轴的夹角小于
轴的夹角小于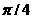 的概率.
的概率.
解析:半圆域如图
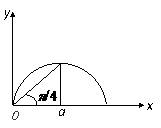 设
设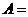 ‘原点与该点连线与
‘原点与该点连线与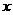 轴夹角小于
轴夹角小于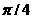 ’
’
由几何概率的定义
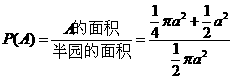
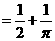 。
。
例10.随机地取两个正数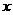 和
和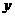 ,这两个数中的每一个都不超过1,试求
,这两个数中的每一个都不超过1,试求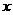 与
与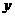 之和不超过1,积不小于0.09的概率.
之和不超过1,积不小于0.09的概率.
解析: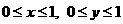 ,不等式确定平面域
,不等式确定平面域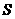 。
。
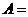 ‘
‘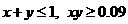 ’则
’则 发生的充要条件为
发生的充要条件为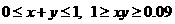 不
不
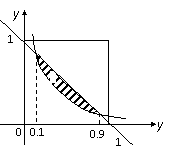 等式确定了
等式确定了 的子域
的子域 ,
,
故:
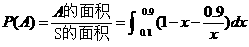
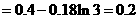
例11. 曲线y=-x2+1与x轴、y轴围成一个区域A,直线x=1、直线y=1、x轴围成一个正方形,向正方形中随机地撒一把芝麻,利用计算机来模拟这个试验,并统计出落在区域A内的芝麻数与落在正方形中的芝麻数
答案:如下表,由计算机产生两例0~1之间的随机数,它们分别表示随机点(x,y)的坐标。如果一个点(x,y)满足y≤-x2+1,就表示这个点落在区域A内,在下表中最后一列相应地就填上1,否则填0。
|
x |
y |
计数 |
|
0.598895 |
0.940794 |
0 |
|
0.512284 |
0.118961 |
1 |
|
0.496841 |
0.784417 |
0 |
|
0.112796 |
0.690634 |
1 |
|
0.359600 |
0.371441 |
1 |
|
0.101260 |
0.650512 |
1 |
|
… |
… |
… |
|
0.947386 |
0.902127 |
0 |
|
0.117618 |
0.305673 |
1 |
|
0.516465 |
0.222907 |
1 |
|
0.596393 |
0.969695 |
0 |
5.几种常见的几何概型
(1)设线段l是线段L的一部分,向线段L上任投一点.若落在线段l上的点数与线段L的长度成正比,而与线段l在线段l上的相对位置无关,则点落在线段l上的概率为:
P=l的长度/L的长度
(2)设平面区域g是平面区域G的一部分,向区域G上任投一点,若落在区域g上的点数与区域g的面积成正比,而与区域g在区域G上的相对位置无关,则点落在区域g上概率为:
P=g的面积/G的面积
(3)设空间区域上v是空间区域V的一部分,向区域V上任投一点.若落在区域v上的点数与区域v的体积成正比,而与区域v在区域v上的相对位置无关,则点落在区域V上的概率为:
P=v的体积/V的体积
4.几何概型的概率公式:
P(A)= 。
。
3.几何概型的概念
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型;
2.随机数的产生方法
(1)利用函数计算器可以得到0~1之间的随机数;
(2)在Scilab语言中,应用不同的函数可产生0~1或a~b之间的随机数。
1.随机数的概念
随机数是在一定范围内随机产生的数,并且得到这个范围内任何一个数的机会是均等的。
本讲内容在高考中所占比较轻,纵贯近几年的高考对概率要求降低,但本讲内容使新加内容,考试涉及的可能性较大
预测2010年高考:
(1)题目类型多以选择题、填空题形式出现,;
(2)本建考试的重点内容几何概型的求值问题,我们要善于将实际问题转化为概率模型处理。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com