7. (12分)设P:函数y =ax²－2x+1在［1,+∞)内单调递减,Q：曲线y=x²－2ax+4a+5与x轴没有交点；如果“﹁P或Q”为真，“﹁P且Q”为假，求a的取值范围. 　

6．(13分)设函数f(x)=p(x-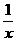)-2lnx,g(x)=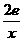(p是实数，e为自然对数的底数)

　 (1)若f(x)在其定义域内为单调函数，求p的取值范围；

　 (2)若直线l与函数f(x),g(x)的图象都相切，且与函数f(x)的图象相切于点(1，0)，求p的值；

　 (3)若在[1，e]上至少存在一点x₀，使得f(x₀)＞g(x₀)成立，求p的取值范围. 　

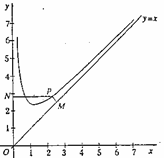
5．(13分)已知函数f(x)=x+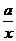的定义域为(0，+∞)且f(2)=2+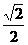，设点P是函数图象上的任意一点，过点P分别作直线y=x和y轴的垂线，垂足分别为M，N. 　

　 (1)求a的值；

　 (2)问：|PM|·|PN|是否为定值？若是，则求出该定值，若不是，则说明理由：

　 (3)设O为坐标原点，求四边形OMPN面积的最小值。

4．(12分)

在△ABC中，∠A ．∠B．∠C所对的边分别为a．b．c。

若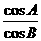=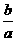且sinC=cosA 　

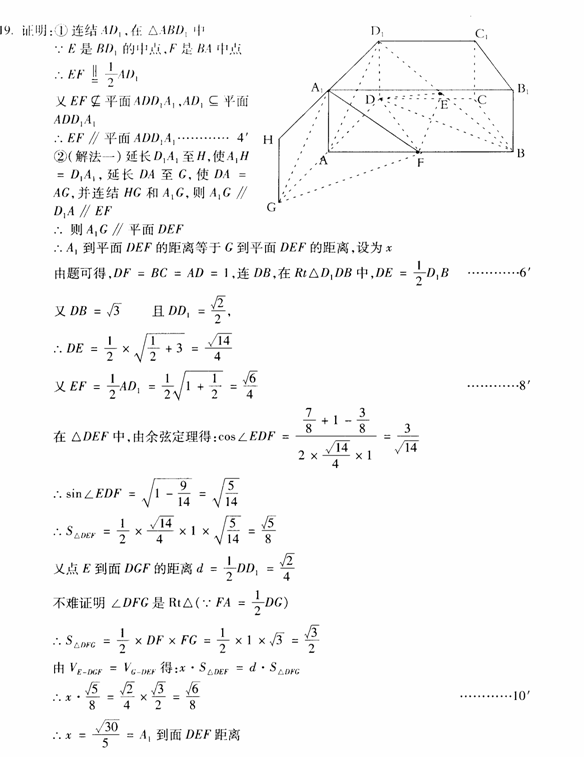
　 (1)求角A．B．C的大小；

　 (2)设函数f(x)=sin(2x+A)+cos(2x-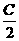),求函数f(x)的单调递增区间，并指出它相邻两对称轴间的距离。

3．(13分)某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力，每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训.已知参加过财会培训的有60%，参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响.

(Ⅰ)任选1名下岗人员，求该人参加过培训的概率；

(Ⅱ)任选3名下岗人员，求这3人中至少有2人参加过培训的概率. 　

2．(12分) 在如图所示的几何体中，EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，且AC=BC=BD=2AE，M是AB的中点.

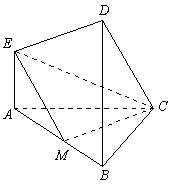
　　 (I)求证：CM ⊥EM：　

　　 (Ⅱ)求DE与平面EMC所成角的正切值.

1．(12分)已知向量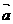=(sinθ，cosθ-2sinθ)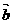，=(1，2)

　 (1)若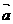⊥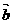，求tanθ的值；

　 (2)若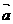∥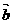，且θ为第Ⅲ象限角，求sinθ和cosθ的值。

6．解：(1)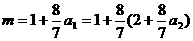

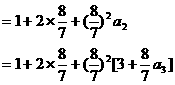
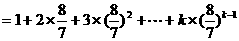　 ①　　　　　　　　　　　　　　 …………2分

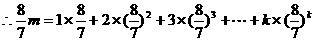②

由①-②得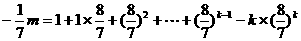…………4分

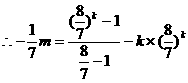
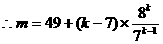　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………6分

　 (2)由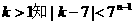

又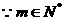故此有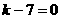

故k=7，m=49　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………9分

　 (3)

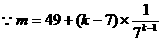
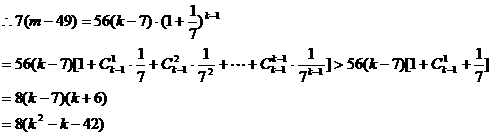
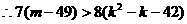　　 　　　 …………14分

5．解：(1)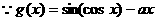

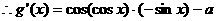
依题意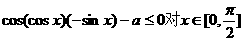恒成立

即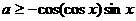

显然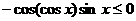

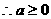，故a的取值范围是　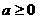　　　　　　　　　　　　　　　　　　　　 …………6分

　 (2)由(1)知：当a=1时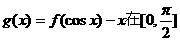，上是减函数

且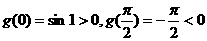

∴存在唯一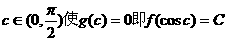　　　　　　　　　　 …………8分

同理由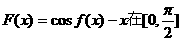上是减函数

且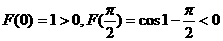

知存在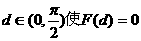

即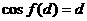成立　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………10分

由

及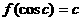的唯一性知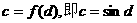

综上可知，存在c，d使同时成立，

且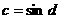　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………13分

4．解：(1)设M(0，m)，N(0，n)，P(x，y)

则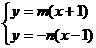

两式相乘得：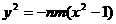

连MB、NB，则MB⊥NB，在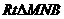中

知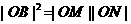

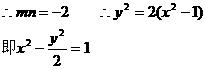
故P的轨迹方程为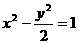　　　　　　　　　　　　　　　　　　　　　　　 …………6分

　 (2)当直线GH与x轴垂直时，设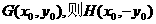

从而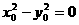

又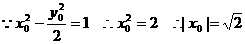

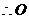　　 到直线GH的距离为　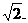　　　　　　　　　　　　　　　　　　　　　　　 …………8分

当直线与x轴不垂直时，设其方程为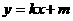

代入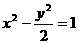并整理得：

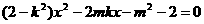
设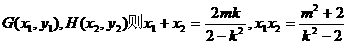　　 …(*)……9分

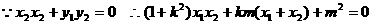
将(*)代入并整理和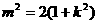

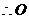到GH的距离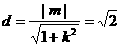

故O到GH的距离为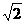　　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………12分