
题目列表(包括答案和解析)
7.用数学归纳法证明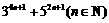 能被8整除时,当
能被8整除时,当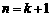 时,对于
时,对于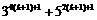 可变形为( )
可变形为( )
A.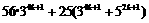 B.
B.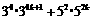
C.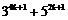 D.
D.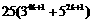
6.用数学归纳法证明不等式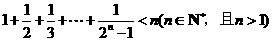 时,不等式在
时,不等式在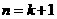 时的形式是( )
时的形式是( )
A.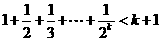
B.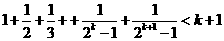
C.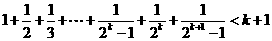
D.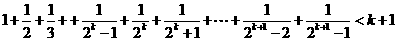
5.用数学归纳法证明,“当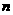 为正奇数时,
为正奇数时,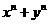 能被
能被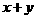 整除”时,第二步归纳假设应写成( )
整除”时,第二步归纳假设应写成( )
A.假设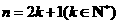 时正确,再推证
时正确,再推证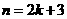 正确
正确
B.假设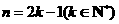 时正确,再推证
时正确,再推证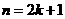 正确
正确
C.假设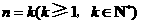 的正确,再推证
的正确,再推证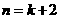 正确
正确
D.假设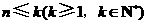 时正确,再推证
时正确,再推证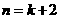 正确
正确
4.如果命题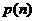 对
对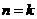 成立,那么它对
成立,那么它对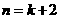 也成立,又若
也成立,又若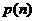 对
对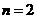 成立,则下列结论正确的是( )
成立,则下列结论正确的是( )
A.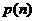 对所有自然数
对所有自然数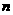 成立
成立
B.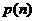 对所有正偶数
对所有正偶数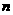 成立
成立
C.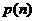 对所有正奇数
对所有正奇数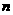 成立
成立
D.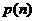 对所有大于1的自然数
对所有大于1的自然数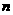 成立
成立
3.已知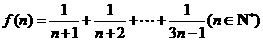 ,则
,则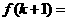 ( )
( )
A.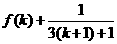
B.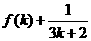
C.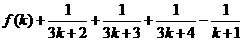
D.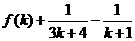
2.凸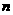 边形有
边形有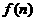 条对角线,则凸
条对角线,则凸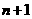 边形的对角线的条数
边形的对角线的条数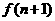 为( )
为( )
A.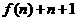 B.
B.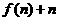 C.
C.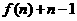 D.
D.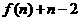
1.用数学归纳法证明“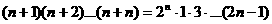 ”从
”从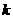 到
到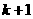 左端需增乘的代数式为 ( )
左端需增乘的代数式为 ( )
A.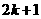 B.
B.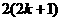 C.
C.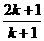 D.
D.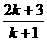
18.设函数f(x)=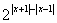 ,求使f(x)≥2
,求使f(x)≥2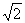 的x的取值范围.
的x的取值范围.

17.设函数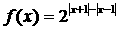 ,求使
,求使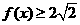 的
的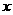 取值范围.
取值范围.
16.点(2,1)与(1,2)在函数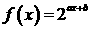 的图象上,求
的图象上,求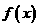 的解析式
的解析式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com