
题目列表(包括答案和解析)
4、(2009昆明一中第三次模拟)设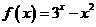 ,则在下列区间中,使函数
,则在下列区间中,使函数 有零点的区间是( )
有零点的区间是( )
A. 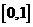 B
B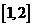 C.
C. 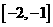 D.
D.
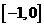
答案 D
3、(2009滨州一模)设函数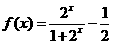 ,
, 表示不超过
表示不超过 的最大整数,则函数
的最大整数,则函数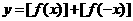 的值域为
的值域为
A .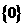 B .
B .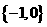 C .
C . 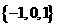 D .
D . 
答案 B
2、(2009昆明市期末)函数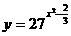 的最小值是 ( )
的最小值是 ( )
A.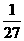 B.
B.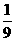 C.9 D.27
C.9 D.27
答案 B
1、(2009广东三校一模)2.函数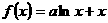 在
在 处取到极值,则
处取到极值,则 的值为
的值为
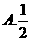
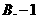
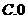
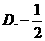
答案 B
4. (哈师大附中、东北师大附中、辽宁省实验中学)已知函数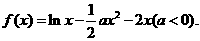
(1)若函数 在定义域内单调递增,求
在定义域内单调递增,求 的取值范围;
的取值范围;
(2)若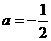 且关于x的方程
且关于x的方程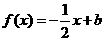 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)设各项为正的数列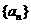 满足:
满足: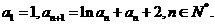 求证:
求证: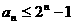
解:(1)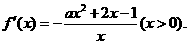
依题意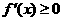 在
在 时恒成立,即
时恒成立,即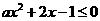 在
在 恒成立.
恒成立.
则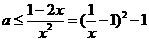 在
在 恒成立,即
恒成立,即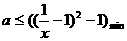
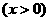
当 时,
时,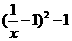 取最小值
取最小值
∴ 的取值范围是
的取值范围是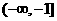 ……
……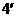
(2)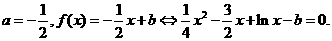
设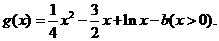 则
则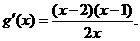 列表:
列表:
 |
 |
 |
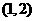 |
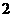 |
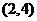 |
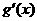 |
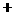 |
 |
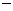 |
 |
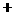 |
 |
|
极大值 |
¯ |
极小值 |
|
∴ 极小值
极小值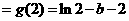 ,
, 极大值
极大值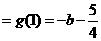 ,又
,又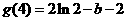 ……
……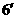
 方程
方程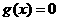 在[1,4]上恰有两个不相等的实数根.
在[1,4]上恰有两个不相等的实数根.
则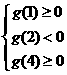 , 得
, 得 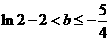 …………
…………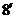
(3)设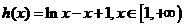 ,则
,则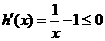
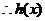 在
在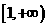 为减函数,且
为减函数,且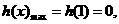 故当
故当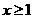 时有
时有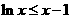 .
.
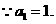 假设
假设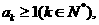 则
则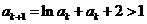 ,故
,故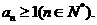
从而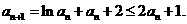
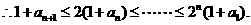
即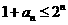 ,∴
,∴ …………
…………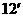
3. (安庆市四校元旦联考)(满分16分)设函数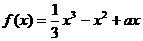 ,
,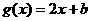 ,当
,当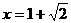 时,
时, 取得极值。
取得极值。
⑴求 的值,并判断
的值,并判断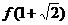 是函数
是函数 的极大值还是极小值;
的极大值还是极小值;
⑵当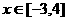 时,函数
时,函数 与
与 的图象有两个公共点,求
的图象有两个公共点,求 的取值范围。
的取值范围。
解:(1)由题意 
 当
当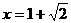 时,
时, 取得极值,
取得极值,
 所以
所以 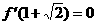
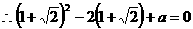
 即
即 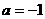
此时当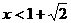 时,
时,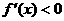 ,当
,当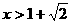 时,
时,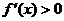 ,
,
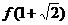 是函数
是函数 的最小值。
的最小值。
(2)设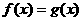 ,则
,则 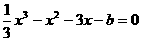 ,
,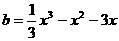
设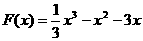 ,
,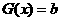
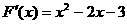 ,令
,令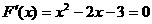 解得
解得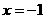 或
或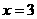
列表如下:
 |
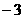 |
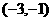 |
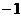 |
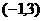 |
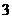 |
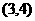 |
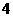 |
 |
|
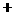 |
 |
__ |
0 |
+ |
|
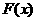 |
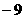 |
  |
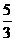 |
  |
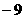 |
 |
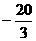 |
 函数
函数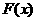 在
在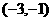 和
和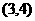 上是增函数,在
上是增函数,在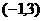 上是减函数。
上是减函数。
当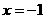 时,
时,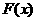 有极大值
有极大值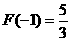 ;当
;当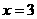 时,
时,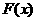 有极小值
有极小值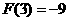
 函数
函数 与
与 的图象有两个公共点,
的图象有两个公共点, 函数
函数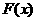 与
与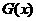 的图象有两个公共点
的图象有两个公共点
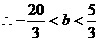 或
或 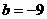
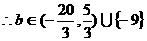
2.(本小题满分13分)已知函数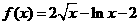 .
.
(I)求 的单调区间;
的单调区间;
(II)若不等式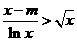 恒成立,求实数
恒成立,求实数 的取值组成的集合.
的取值组成的集合.
解:(I)由已知得 .因为
.因为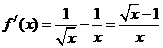 ,……………………2分
,……………………2分
所以当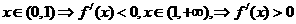 .
.
故区间 为
为 的单调递减区间,
的单调递减区间,
区间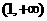 为
为 的单调递增区间.
……………………5分
的单调递增区间.
……………………5分
(II)(i)当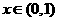 时,
时,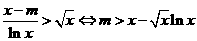 .
.
令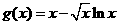 ,则
,则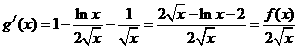 .……7分
.……7分
由(1)知当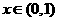 时,有
时,有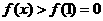 ,所以
,所以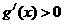 ,
,
即得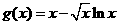 在
在 上为增函数,所以
上为增函数,所以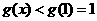 ,
,
所以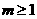 .
……………………10分
.
……………………10分
(ii)当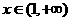 时,
时, .
.
由①可知,当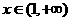 时,
时,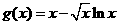 为增函数,所以
为增函数,所以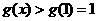 ,
,
所以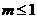 。
。
综合以上,得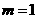 .故实数
.故实数 的取值组成的集合为
的取值组成的集合为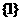 . ……………………13分
. ……………………13分
1.(池州市七校元旦调研)设函数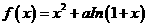 有两个极值点
有两个极值点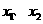 ,且
,且 ,
,
求 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性;
解: (I)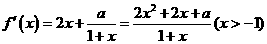
令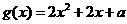 ,其对称轴为
,其对称轴为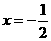 。由题意知
。由题意知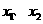 是方程
是方程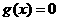 的两个均大于
的两个均大于 的不相等的实根,其充要条件为
的不相等的实根,其充要条件为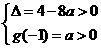 ,得
,得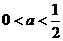
⑴当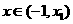 时,
时,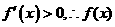 在
在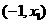 内为增函数;
内为增函数;
⑵当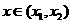 时,
时,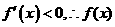 在
在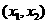 内为减函数;
内为减函数;
⑶当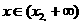 时,
时,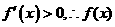 在
在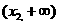 内为增函数;
内为增函数;
2.(安徽两地三校国庆联考)若函数f (x) = 4x3-ax+3的单调递减区间是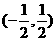 ,则实数a的值为
,则实数a的值为
答案 3
1.
对于任意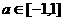 ,函数
,函数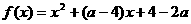 的值恒大于零,那么
的值恒大于零,那么 的取值范围是
.
的取值范围是
.
答案 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com