
题目列表(包括答案和解析)
2.已知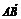 =(2,4,5),
=(2,4,5),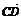 =(3,x,y),若
=(3,x,y),若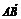 ∥
∥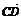 ,则x=
,y=
.
,则x=
,y=
.
答案 6 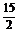
1.若平面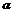 、
、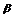 的法向量分别为n1=(2,3,5),n2=(-3,1,-4),则
的法向量分别为n1=(2,3,5),n2=(-3,1,-4),则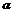 ,
, 的位置关系是 (用“平行”,“垂直”,“相交但不垂直”填空).
的位置关系是 (用“平行”,“垂直”,“相交但不垂直”填空).
答案 相交但不垂直
20.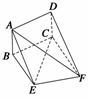 (16分)如图所示,矩形ABCD和梯形BEFC所在平面互相垂直, BE∥CF,
(16分)如图所示,矩形ABCD和梯形BEFC所在平面互相垂直, BE∥CF,
∠BCF=∠CEF=90°,AD=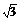 ,EF=2.
,EF=2.
(1)求证:AE∥平面DCF;
(2)当AB的长为何值时,二面角A-EF-C的大小为60°?
19.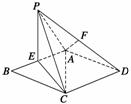 (16分)如图所示,在矩形ABCD中,AB=2BC=2a,E为AB上一点,将B点沿线段EC折起至点P,连接PA、PC、PD,取PD的中点F,若有AF∥平面PEC.
(16分)如图所示,在矩形ABCD中,AB=2BC=2a,E为AB上一点,将B点沿线段EC折起至点P,连接PA、PC、PD,取PD的中点F,若有AF∥平面PEC.
(1)试确定E点位置;
(2)若异面直线PE、CD所成的角为60°,并且PA的长度大于a,
求证:平面PEC⊥平面AECD.
18.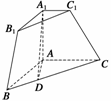 (16分)三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°, A1A⊥平面ABC,A1A=
(16分)三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°, A1A⊥平面ABC,A1A=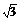 ,AB=
,AB=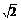 ,AC=2, A1C1=1,
,AC=2, A1C1=1,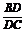 =
=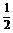 .
.
(1)证明:平面A1AD⊥平面BCC1B1; (2)求二面角A-CC1-B的余弦值.
17.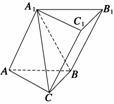 (14分)如图所示,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,
(14分)如图所示,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,
AB⊥BC,CB=3,AB=4,∠A1AB=60°.
(1)求证:平面CA1B⊥平面A1ABB1;
(2)求直线A1C与平面BCC1B1所成角的正切值;
(3)求点C1到平面A1CB的距离.
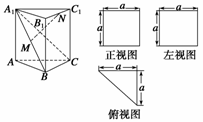
16.(14分)一个多面体的直观图和三视图(正视图、左视图、俯视图)如图所示,M、N分别为A1B、B1C1的中点。
求证:(1)MN∥平面ACC1A1;(2)MN⊥平面A1BC.
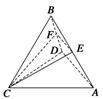
15.(14分)在四面体ABCD中,CB=CD,AD⊥BD,且E,F分别是AB,BD的中点,
求证: (1)直线EF∥平面ACD;(2)平面EFC⊥平面BCD.
14.在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE= .
13.若l、m、n是互不相同的空间直线, 、
、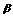 是不重合的平面,则下列命题中为真命题的
是不重合的平面,则下列命题中为真命题的
是 (填序号).
①若 ∥
∥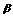 ,l
,l
 ,n
,n
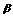 ,则l∥n,②若
,则l∥n,②若 ⊥
⊥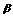 ,l
,l
 ,则l⊥
,则l⊥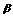
③若l⊥n,m⊥n,则l∥m,④若l⊥ ,l∥
,l∥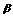 ,则
,则 ⊥
⊥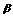
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com