13．求下列函数的值域：

(1)y＝；(2)y＝；

(3)y＝x－；(4)y＝log₃x+log_x3－1.

分析：

解析：(1)解法一：(反函数法)

因为函数y＝的反函数为y＝，后者其定义域为{x|x≠，x∈R}，

故函数的值域为{y|y≠，x∈R}．

解法二：(分离常数法)y＝＝＝－.

∵≠0，∴函数的值域为{y|y≠，y∈R}．

(2)解法一：(配方法)

∵y＝1－，而x²－x+1＝(x－)²+≥，

∴0<≤，∴－≤y<1.

解法二：(判别式法)由y＝，得(y－1)x²+(1－y)x+y＝0，

∵y＝1时，x∈∅，∴y≠1，又∵x∈R，

∴必须△＝(1－y)²－4y(y－1)≥0.∴－≤y≤1.

∵y≠1，∴函数的值域为[－，1)．

(3)解法一：(单调性法)定义域为{x|x≤}，函数y＝x，y＝－，均在(－∞，]上递增，则y＝x－在(－∞，]上递增，故y≤－＝.

解法二：(换元法)令＝t，

则t≥0，且x＝.∴y＝－(t+1)²+1≤(t≥0)，

∴y∈(－∞，]．

(4)当x>1时，log₃x>0，故有y≥2－1＝1.

当且仅当log₃x＝，即log₃x＝1，即x＝3时等号成立．

当0<x<1时，log₃x<0，－log₃x>0

∴y＝log₃x+－1＝－(－log₃x－)－1≤－2－1＝－3.

当且仅当log₃x＝，即x＝时等号成立，

综上可知，函数的值域为{y|y≤－3或y≥1}．

12．(2011·原创题)在实数的原有运算法则中，我们补充定义新运算“?”如下：

当a≥b时，a?b＝a；当a＜b时，a?b＝b².

则函数f(x)＝(1?x)·x－(2?x)(x∈[－2,2])的最大值等于________(“·”和“－”仍为通常的乘法和减法)．

答案：6

解析：当x∈[－2,1]时，f(x)＝1·x－2＝x－2，f(x)_max＝－1；

当x∈(1,2]时，f(x)＝x²·x－2＝x³－2，f(x)_max＝6，故填6.

11．设x、y≥0,2x+y＝6，则Z＝4x³+3xy+y²－6x－3y的最大值是__________，最小值是__________．

答案：18　

分析：转化为一元函数最值，转化时注意挖掘出变元的取值范围(隐含条件)．

解答：由y＝6－2x≥0及x≥0得0≤x≤3，将y＝6－2x代入Z中得Z＝2x²－6x+18(0≤x≤3)，从而解得：

Z_max＝18，Z_min＝.

10．函数y＝log₃(9－x²)的定义域为A，值域为B，则A∩B＝________.

答案：{x|－3<x≤2}

解析：由9－x²>0得－3<x<3，

∴A＝{x|－3<x<3}．

∵0<9－x²≤9，∴log₃(9－x²)≤2.

∴B＝(－∞，2]故A∩B＝{x|－3<x≤2}．

9．(2009·湖北八校第一次联考)函数y＝的值域为________．

答案：(－∞，0)∪(，+∞)

解析：由e^x＝>0⇒y<0或y>.

8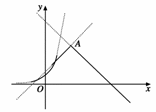．(2009·宁夏、海南，12)用min{a，b，c}表示a、b、c三个数中的最小值．设f(x)＝min{2^x，x+2,10－x}(x≥0)，则f(x)的最大值为　　　　　 (　)

A．4　　 B．5　 　C．6　　 D．7

答案：C

解析：f(x)＝min{2^x，x+2,10－x}(x≥0)的图象如图．令x+2＝10－x，得x＝4.

当x＝4时，f(x)取最大值，f(4)＝6.

7．函数f(x)＝2－(0≤x≤4)的值域是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．[－2,2]　 　　　　　　　　　　　　　　 B．[1,2]

C．[0,2]　 　　　　　　　　　　　　　　　　 D．{－，}

答案：C

解析：用三角换元法，可令x－2＝2sinθ，θ∈[－，]．

∵y＝2－＝2－

∴y＝2－2cosθ∈[0,2]，故选C.

6．(2009·重庆市高三联合诊断性考试(第一次))已知函数y＝x²－3x+3(x>0)的值域是[1,7]，则x的取值范围是　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(0,4]　 　　　　　　　　　　　　　　　　 B．[1,4]

C．[1,2]　 　　　　　　　　　　　　　　　　 D．(0,1]∪[2,4]

答案：D

解析：依题意得y＝(x－)²+(x>0)的值域是[1,7]，由x²－3x+3＝1解得x＝1或x＝2；由x²－3x+3＝7得x＝－1(舍)或x＝4.结合该函数的图象分析可知，x的取值范围是(0,1]∪[2,4]，选D.

5．函数y＝的定义域是(－∞，1)∪[2,5)，则其值域是　　　　　　　　　　　　　　　 (　)

A．(－∞，0)∪(，2]

B．(－∞，2]

C．(－∞，)∪[2，+∞)

D．(0，+∞)

答案：A

解析：∵x∈(－∞，1)∪[2,5)，则x－1∈(－∞，0)∪[1,4)，∴∈(－∞，0)∪(，2]，故应选A.

4．(2009·湖北部分重点中学第二次联考)函数y＝(x>0)的值域是　　　　　 (　)

A．(0，+∞)　　　　 　　 B．(0，)

C．(0，]　 　　　　　　　　　　　　　　　 D．[，+∞)

答案：C

解析：由y＝(x>0)得0<y＝＝≤＝，因此该函数的值域是(0，]，故选C.