11．已知f(x)＝log₄(2x+3－x²)，

(1)求函数f(x)的单调区间；

(2)求函数f(x)的最大值，并求取得最大值时的x的值．

解：(1)单调递增区间为(－1,1]，递减区间为[1,3)

(2)因为μ＝－(x－1)²+4≤4，

所以y＝log₄μ≤log₄4＝1，

所以当x＝1时，f(x)取最大值1.

评析：在研究函数的性质时，要在定义域内研究问题，定义域“优先”在对数函数中体现的更明确．

10．若函数f(x)＝^{lg(ax2－x+1)}的值域是(0，+∞)，则实数a的取值范围是________．

解析：令t＝lg(ax²－x+1)，

则y＝^t的值域是(0，+∞)，

∴t应取到每一个实数，

即函数t＝lg(ax²－x+1)的值域为R.

当a＝0时，t＝lg(－x+1)的值域为R，适合题意，

当a≠0时，应有⇒0<a≤.

综上，a的取值范围是0≤a≤.

答案：0≤a≤

9．已知f(3^x)＝4xlog₂3+233，则f(2)+f(4)+f(8)+…+f(2⁸)的值等于________．

解析：∵f(3^x)＝4xlog₂3+233＝4log₂3^x+233，

∴f(2)+f(4)+…+f(2⁸)＝4(1+2+…+8)+233×8＝2008.

答案：2008

8．(2010·潍坊检测)函数f(x)＝ln(a≠2)为奇函数，则实数a等于________．

解析：依题意有f(－x)+f(x)＝ln+ln＝0，即·＝1，故1－a²x²＝1－4x²，解得a²＝4，但a≠2，故a＝－2.

答案：－2

7．函数y＝的定义域是________．

解析：由题意知，log_0.5(4x²－3x)≥0＝log_0.51，

由于0<0.5<1，所以

从而可得函数的定义域为∪.

答案：∪

6．(2010·浙江)设函数的集合P＝{f(x)＝log₂(x+a)+b|a＝－，0，，1；b＝－1,0,1}，平面上点的集合Q＝{(x，y)|x＝－，0，，1；y＝－1,0,1}，则在同一直角坐标系中，P中函数f(x)的图象恰好经过Q中两个点的函数的个数是(　)

A．4　　　B．6　 C．8　　　D．10

解析：集合P中的元素共12个．当a＝－时，f₁(x)＝log₂－1，f₂(x)＝log₂，f₃(x)＝log₂+1，当x＝1时，这三个函数都不可能经过集合Q中的两个点；当a＝0时，f₄(x)＝log₂x－1，f₅(x)＝log₂x，f₆(x)＝log₂x+1，此时只有后面两个函数恰好经过集合Q中的两个点；当a＝时，f₇(x)＝log₂－1，f₈(x)＝log₂，f₉(x)＝log₂+1，此时只有后面两个函数经过集合Q中的两个点；当a＝1时，f₁₀(x)＝log₂(x+1)－1，f₁₁(x)＝log₂(x+1)，f₁₂(x)＝log₂(x+1)+1，此时f₁₀(x)经过集合Q中的两个点(0，－1)，(1,0)，f₁₁(x)经过集合Q中的三个点，(0,0)，(1,1)，函数f₁₂(x)经过集合Q中的点，(0,1)．综上可知集合P中只有6个元素满足题意．

答案：B

5．(2010·全国Ⅰ)设a＝log₃2，b＝ln2，c＝5^－，则(　)

A．a<b<c　 B．b<c<a

C．c<a<b　 D．c<b<a

解析：a＝log₃2＝<ln2＝b，又c＝5^－＝<，a＝log₃2>log₃＝，因此c<a<b，故选C.

答案：C

4．(2010·全国Ⅰ)已知函数f(x)＝|lgx|，若a≠b，且f(a)＝f(b)，则a+b的取值范围是(　)

A．(1，+∞)　 B．[1，+∞)

C．(2，+∞)　 D．[2，+∞)

解析：不妨设0<a<1<b，由f(a)＝f(b)得－lga＝lgb，lga+lgb＝0，ab＝1，因此，a+b＝a+>2，故选C.

答案：C

3．(2010·潍坊市质检)函数f(x)＝log₂x的图象的大致形状是(　)

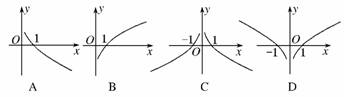
解析：先化简函数解析式，再根据解析式研究函数性质进行判断．由于f(x)＝log₂x ＝log₂|x|，所以函数的定义域是(－∞，0)∪(0，+∞)，且当x>0时，f(x)＝log₂x在(0，+∞)上单调递增，又函数是偶函数，所以函数图象关于y轴对称，因此选D.

答案：D

评析：像这样“给式选图”题一般是通过解析式研究函数的性质(例如函数的定义域、值域、奇偶性、单调性)，及其在函数图象上的特征进行选择．

2．(运算题，中)已知函数f(x)＝则f(2+log₂3)的值为(　)

A.　　B.　 C.　　D.

答案：D