11．解析：依据两点之间线段最短，确定最短路线为长方形公园的对角线长，可设长方形公园的对角线长为x米，由勾股定理得：x²＝120²+350²，解得x=370．

答案：370．

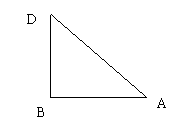
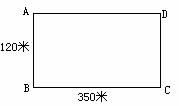
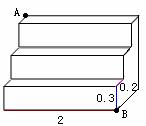
　　　　　　 图8　　　　　　　　　　 图9　　　　　　 图10　

10．解析：由题意可知梯子的长是不变的，由云梯长10米 ，梯子顶端离地面6米，可由勾股定理求得梯子的底部距墙8米．当梯子顶端离地面8米时， 梯子的底部距墙为6米，则梯子的底部在水平面方向要向左滑动8-6=2(米)．

答案：2．

9．解析：由题意可知AB、DC为3m，BC为4m，由勾股定理得：

AC²＝AB²+BC²＝3²+4²=25=5²，所以AC=5．

答案：5．

8．解析：延长AB、DC构成直角三角形，运用勾股定理得

BC²＝(15-3)²+(20-4)²＝12²+16²=400，所以BC=20．

答案：20cm．

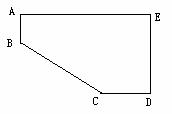
　　　　 　　　图5　　　　　　　　　 图6　　　　　　　　　 图7

7．解析：如图4，把实际问题转化为数学模型，

由题意可知AB=1200,AC=2000,

由勾股定理得：

BC²=AC²－AB²= 2000²-1200²=1600² ，

所以BC=1600．李明向正东方向走了1600米．

答案：1600．

6．解析：在长方体的盒子中，一角的顶点与斜对的不共面的顶点的距离最大．

因此可设放入长方体盒子中的最大长度是x㎝，

根据题意，得x² ＝50²+40 ² +30²＝5000．70² ＝4900，

因为4900＜5000,所以能放进去．

答案：能．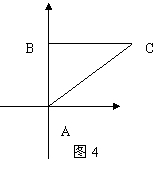

5．解析：如图，此题可运用勾股定理解决，设这条木板的长度为x米，

由勾股定理得：x²＝1.5²+3.6²，解得x=3.9．

答案： B ．

4．解析：等腰三角形的高把等腰三角形分成两个直角三角形, 腰为斜边,高和底边长一半为直角边,因此由三角形三边关系及勾股定理可知A. 13²≠12²+6²， B. 12²≠8²+6² ，C.13²=12²+5² ， D.5²≠4²+4².

答案：C．

3．解析：因为平面展开图不唯一,故分情况分别计算,进行大、小比较，再从各个路线中确定最短的路线．(1)展开前面右面由勾股定理得AB²＝；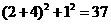

(2) 展开前面上面由勾股定理得AB²＝；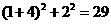

(3)展开左面上面由勾股定理得AB²＝；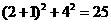

所以最短路径的长为．

答案：A．

2．解析：13米长的梯子可以达到建筑物的高度可设为x米，　　

因梯子的底端离建筑物5米，由勾股定理得：

x²=13²-5²，x=12米．

答案：A ．