23.在直角坐标中，A在x轴正半轴上，OA＝4，B(4,4)，点E从0出发沿x轴正半轴运动，点F从0点出发，沿x轴负半轴运动，以BE为直径作⊙O₁，BF与y轴交于C。

(1)若E以1个单位/秒，点F以4单位/秒的速度同时出发，问经过几秒钟，⊙O₁与y轴相切于C点？

(2)若E以1个单位/秒，点F以m单位/秒的速度同时出发，E在OA内运动，经过2秒钟，直线CE与⊙O1相切，试求直线BC的解析式，并求点F的速度。

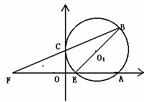(3)若E、F两点同时出发，点E以1个单位/秒，点F以恰当的速度运动，保持OE＝OC，点E在OA内，连AC交⊙O1于P ，试问AP·AC的值是否发生变化？若不变，请说明理由并求值，若变化，说明变化范围？

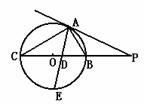
22.△ABC的内接三角形，AC>AB，BC为⊙O的直径，P为AB延长线上的点，且PA²＝PB·PC，∠BAC的平分线交BC于D，交⊙O于E，

(1)　　 求证：PA是⊙O的切线

(2)　　 若⊙O的直径为10，且AD、AE是方程x²－mx+48=0的两根，求tan∠PAB值

21. 某童装厂现有甲种布料38米，乙种布料26米，现计划用这两种布料生产L、M两种型号的童装共50套，已知做一套L型号的童装需用甲种布料0.5米，乙种布料1米，可获利45元；做一套M型号的童装需用甲种布料0.9米，乙种布料0.2米，可获利30元，设生产L型号的童装套数为x，用这批布料生产这两种型号的童装所获利润为y(元)。

(1)写出y关于x的函数解析式，并求出自变量x’的取值范围。

(2)该厂在生产这批童装中，当L型号的童装为多少套时，能使该厂所获的利润最大？最大利润是多少？

20. PA为⊙O的切线，A为切点，PBC为割线，∠APC的平分线PF交AC于F，交AB于E。

(1)　　 求证：AE=AF

(2)　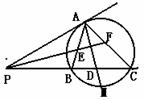　 若PB:PA=1:2，M是BC上的点，AM交BC于D，PD＝DC，试确定M点在BC上的位置，并证明你的结论。

19.一次函数y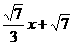＝　 的图象分别与x轴y轴交于A、B，设有点C(a，0)，且a<0有△ABC为等腰三角形，求经过B 、C两点的直线的解析式。

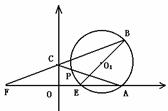
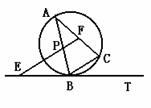
18. 已知△ABC是⊙O的内接三角形，BT为⊙O切线，B为切点，P为直线AB上的一点，过P 作BC的平行线交直线BT于E，交直线AC于F，

(1)　　 当P在线段AB上时，求证：PA·PB=PE·PF

(2)　　 点P在线段BA的延长线上时，第(1)题 的结论还成立吗？如果成立，请画图证明；如果不成立，请说明理由。

17.直线y＝3x+b和两坐标轴成三角形的面积等于24，求b

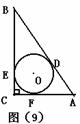
16.如图(9)，在Rt△ABC中，⊙O分别切AB、BC、AC于D、E、F三点，AB=10，∠A的余弦值为3/5，则S_⊙O=　　　　　　

15.点P不在⊙O上，过P的直线交⊙O于AB，若PA.PB=24，OP=5，则⊙O的半径长为　　　

14.如图(8)在直角坐标系中，⊙C与y轴相切与x轴相交于(1, 0)，(5, 0)两点，圆心C在第四象限，则C点坐标为(　　　　　 )