27．已知抛物线y=-x²-2kx+3k²(k>0)交x轴于A、B两点,交y轴于点C,以AB 为直径的⊙E交y轴于点D、F(如图),且DF=4,G 是劣弧A D上的动点(不与点A、D重合),直线CG交x轴于点P.

(1)　　 求抛物线的解析式;

(2)　　 当直线 CG是⊙E的切线时,求tan∠PCO的值.

(3)　　

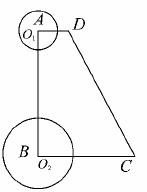
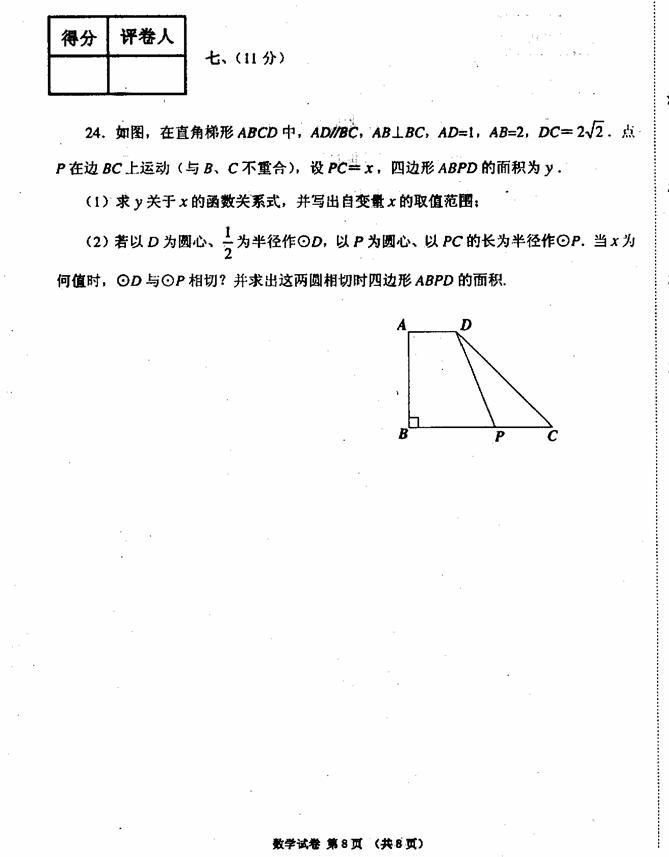
如图,已知直角梯形ABCD中，AD∥BC，∠A=90^o，∠C=60^o，AD=3cm，BC=9cm．⊙O₁的圆心O₁从点A开始沿A-D-C折线以1cm/s的速度向点C运动，⊙O₂的圆心O₂从点B开始沿BA边以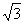cm/s的速度向点A运动，如果⊙O₁半径为2cm，⊙O₂的半径为4cm，若O₁、O₂分别从点A、点B同时出发，运动的时间为ts

　　 (1)请求出⊙O₂与腰CD相切时t的值；

　　 (2)在0s<t≤3s范围内，当t为何值时，⊙O₁与⊙O₂外切？

22、某课外学习小组在设计一个长方形时钟钟面时，欲使长方形的宽为20厘米，时钟的中心在长方形对角线的交点上，数字2在长方形的顶点上，数字3、6、9、12标在所在边的中点上，如图所示。

(1)问长方形的长应为多少？

(2)请你在长方框上点出数字1的位置，并说明确定该位置的方法；

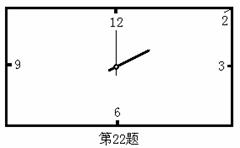(3)请你在长方框上点出钟面上其余数字的位置，并写出相应的数字(说明：要画出必要的，反映解题思路的辅助线)。

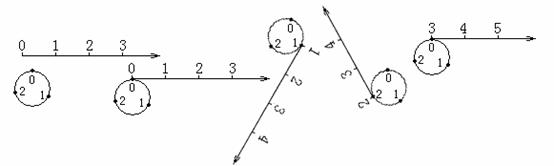
10、如下图所示，按下列方法将数轴的正半轴绕在一个圆上(该圆周长为3个单位长，且在圆周的三等分点处分别标上了数字0、1、2)上：先让原点与圆周上0所对应的点重合，再将正半轴按顺时针方向绕在该圆周上，使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合。这样，正半轴上的整数就与圆周上的数字建立了一种对应关系。

(1)圆周上数字a 与数轴上的数5对应，则a＝_________；

(2)数轴上的一个整数点刚刚绕过圆周n圈(n为正整数)后，并落在圆周上数字1所对应的位置，这个整数是_________(用含n的代数式表示)。

(提醒：后面还有题目，请不要在此停留过长时间)

23、某小型开关厂今年准备投入一定的经费用于现有生产设备的改造以提高经济效益．通过测算：今年开关的年产量y(万只)与投入的改造经费x(万元)之间满足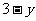与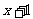成反比例，且当改造经费投入1万元时，今年的年产量是2万只．

(1)求年产量y(万只)与改造经费x(万元)之间的函数解析式．(不要求写出x的取值范围)

(2)已知每生产1万只开关所需要的材料费是8万元．除材料费外，今年在生产中，全年还需支付出2万元的固定费用．

①求平均每只开关所需的生产费用为多少元．(用含y的代数式表示)

(生产费用=固定费用+材料费)

②如果将每只开关的销售价定位“平均每只开关的生产费用的1.5倍”与“平均每只开关所占改造费用的一半”之和，那么今年生产的开关正好销完．问今年需投入多少改造经费，才能使今年的销售利润为9.5万元？

(销售利润=销售收入－生产费用－改造费用)

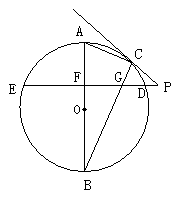
24、如图，AB是⊙O的直径，BC是⊙O的弦，⊙O的割线PDE垂直AB于点F，交BC于点G，连结PC，∠BAC=∠BCP，求解下列问题：

(1)求证：CP是⊙O的切线。

(2)当∠ABC=30°，B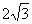G=，CG=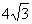时，求以PD、PE的长为两根的一元二次方程。

(3)若(1)的条件不变，当点C在劣弧AD上运动时，应再具备什么条件可使结论BG²=BF·BO成立？试写出你的猜想，并说明理由。

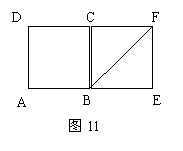
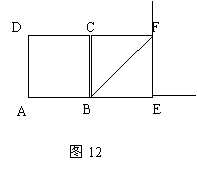
24、如图11，正方形ABCD和正方形BEFC。

操作：M是线段AB上一动点，从A点至B点移动，DM⊥MN，交对角线BF于点N。

探究：线段DM和MN之间的关系，并加以证明。

说明：如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来(要求至少写3步)；(2)在你经历说明(1)的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明。注意：选取①完成证明得9分；选取②完成证明得6分。①M是线段AB的中点；②M、N分别是线段AB、BF的中点。

附加题

如图12，当M是线段AE延长线上一动点，DM⊥MN，交对角线BF延长线于点N，探究线段DM和MN之间的关系，并加以证明。

	A

26、现有含盐15%的盐水20克，含盐40%的盐水15克，另有足够的纯盐和水，要配制成含盐20%的盐水30克。

(1)　　　 试设计一种配制方案；

(2)　　　 试设计一种用纯盐最省的方案；

(3)　　　 试设计一种现有盐水浪费最少的方案。

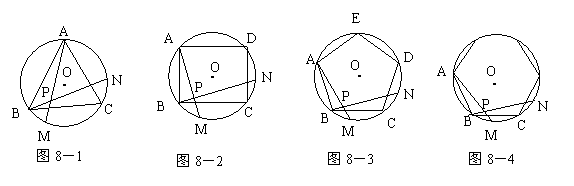
20、如图，8－1、8－2、8－3、…、8－n分别是⊙O的内接正三角形ABC，正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…，点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。

(1)　　　 求图8－1中∠APN的度数；

(2)　　　 图8－2中，∠APN的度数是_______，图8－3中∠APN的度数是________。

(3)　　　 试探索∠APN的度数与正多边形边数n的关系(直接写答案)

26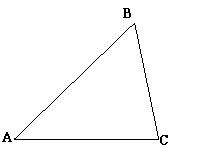．在三角形ABC中，∠B=60°，BA=24cm，BC=16cm。现有动点P从点A出发，沿射线AB向点B方向运动，东点Q从点C出发，沿射线CB也向点B方向运动。如果点P的速度是4cm/秒，点Q的速度是2cm/秒，它们同时出发，求：(1)几秒钟后，△PBQ的面积是△ABC面积的一半？(2)在第(1)问的前提下，P，Q两点之间的距离是多少？

25．为了参加市科技节展览，同学们制造了一个截面为抛物线形的隧道模型，用了三种正方形的钢筋支架，在画设计图时，如果在直角坐标系中，抛物线的函数解析式为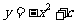，正方形ABCD的边长和正方形EFGH的边长之比为5：1，求：(1)抛物线的解析式中常数c的值。

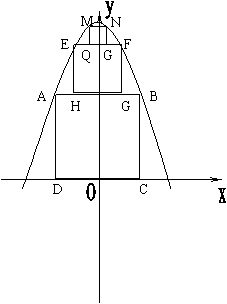(2)正方形MNPQ的边长。