
题目列表(包括答案和解析)
1.(荆州)观察下列各式
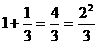 ,
,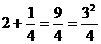 ,
,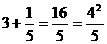 ,
,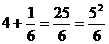 ……
……
设n为正整数,请用关于n的等式表示这个规律为: + =
2(宜昌)观察下列不等式,猜想规律并填空:
1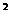 +
2
+
2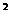 > 2×1×2;
(
> 2×1×2;
(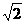 )
)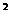 +(
+(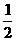 )
)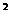 > 2×
> 2×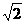 ×
×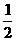
(- 2)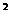 + 3
+ 3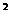 > 2×(-2)×3;
> 2×(-2)×3;
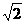
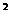 +
+ 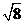
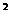 > 2×
> 2×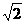 ×
×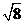
(- 4)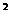 + (-3)
+ (-3)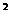 > 2×(-4)×(-3);
(-
> 2×(-4)×(-3);
(-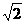 )
)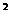 +
(
+
(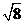 )
)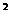 >
2×
>
2×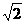 ×
×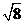
a + b > _____________(a≠b)
3(茂名)下面是用棋子摆成的“上”字:
 第一个“上”字 第二个“上”字
第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和
枚棋子;(2分)
(2)第n个“上”字需用
枚棋子.(1分)
第一个“上”字 第二个“上”字
第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和
枚棋子;(2分)
(2)第n个“上”字需用
枚棋子.(1分)
4(青海).请先观察下列算式,再填空:
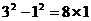 ,
, 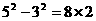 .
(1)
.
(1)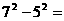 8×
;
(2)
8×
;
(2)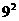 -( )
-( )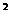 =8×4;
(3)( )
=8×4;
(3)( )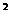 -9
-9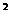 =8×5;
(4)
=8×5;
(4)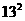 -( )
-( )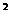 =8× ;……
通过观察归纳,写出反映这种规律的一般结论:
。
=8× ;……
通过观察归纳,写出反映这种规律的一般结论:
。
5(滨州)下图是某同学在沙滩上用石于摆成的小房子.
 观察图形的变化规律,写出第n个小房子用了
块石子
观察图形的变化规律,写出第n个小房子用了
块石子
6(山东)下面是按照一定规律画出的一列“树型”图:

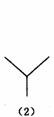
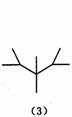
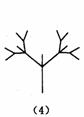
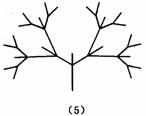
 经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出
个“树枝”.
经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出
个“树枝”.
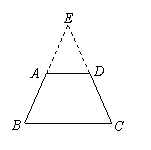
7(烟台)细心观察图形,认真分析各式,然后解答问题。
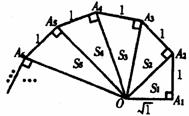
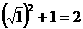
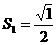
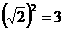
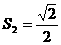
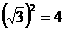
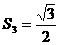 ……
……
(1)请用含有n(n是正整数)的等式表示上述变化规律.
(2)推算出
……
……
(1)请用含有n(n是正整数)的等式表示上述变化规律.
(2)推算出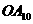 的长.
(3)求出
的长.
(3)求出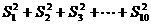 的值.
的值.
8(泰州)(本题设置两个小题,要求只选做一个,多做不加分)
(1)用计算器探索:
①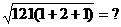 ②
②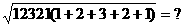 ③
③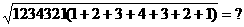 由此猜想:
由此猜想:
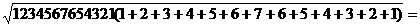 .
(2)已知关于x的方程
.
(2)已知关于x的方程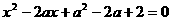 的两个实数根
的两个实数根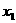 、
、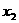 满足
满足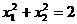 ,则a的值为
。
,则a的值为
。
9(武汉)已知: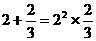 ,
,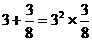 ,
,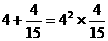 ,…若
,…若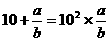 (a、b为正整数),则a+b=
。
(a、b为正整数),则a+b=
。
10(福州)观察下列各式:1×3=12+2×1,
2×4=22+2×2,
3×5=32+2×3,
… …
请你将猜想到的规律用自然数n(n≥1)表示出来: .
11(北京)观察下列顺序排列的等式:
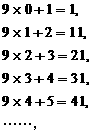
猜想:第n个等式(n为正整数)应为___________________。
12(舟山)古希腊数学家把数1,3,6,10,15,21,……,叫做三角形数,
它有一定的规律性,则第24个三角形数与第22个三角形数的差为
。
13(资阳).如图5,已知四边形ABCD是梯形(标注的数字为边长),按图中所示的规律,用2003个这样的梯形镶嵌而成的四边形的周长是___________.

13(河北)探究规律:如图1,已知直线 ∥
∥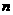 ,A、B为直线
,A、B为直线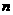 上的两点,C、P为直线
上的两点,C、P为直线 上的两点。
上的两点。
(1)请写出图中面积相等的各对三角形: 。
(2)如果A、B、C为三个定点,点P在 上移动,那么无论P点移动到任何位置总有:
上移动,那么无论P点移动到任何位置总有:
与△ABC的面积相等;
理由是:



解决问题:
如图2,五边形ABCDE是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图3所示的形状,但承包土地与开垦荒地的分界小路(图3中折线CDE)还保留着,张大爷想过E点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多。请你用有关的几何知识,按张大爷的要求设计出修路方案。(不计分界小路与直路的占地面积)
(1)写出设计方案,并在图3中画出相应的图形;
(2)说明方案设计理由。
25. (1)设此一次函数解析式为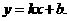 …………………(1分)
…………………(1分)
则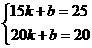 ,解得:k=
,解得:k=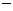 1,b=40,……………………(5分)
1,b=40,……………………(5分)
即:一次函数解析式为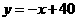 ………………………(6分)
………………………(6分)
(2)设每件产品的销售价应定为x元,所获销售利润为w元…………………………(7分)
w =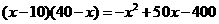
=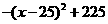 ………………………………………………………………………(10分)
………………………………………………………………………(10分)
产品的销售价应定为25元,此时每日获得最大销售利润为225元……………………(12分)
26(1)证明∵点A1,D1分别是AB、AD的中点,∴A1D1是△ABD的中位线………………(1分)
∴A1D1∥BD,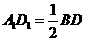 ,同理:B1C1∥BD ,
,同理:B1C1∥BD ,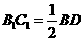 ……………………(2分)
……………………(2分)
∴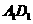 ∥
∥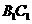 ,
,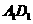 =
=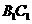 , ∴四边形
, ∴四边形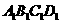 是平行四边形………………(4分)
是平行四边形………………(4分)
∵AC⊥BD,AC∥A1B1,BD∥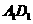 ,∴A1B1⊥
,∴A1B1⊥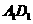 即∠B1A1D1=90°………(5分)
即∠B1A1D1=90°………(5分)
∴四边形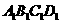 是矩形…………………………………………………………………(6分)
是矩形…………………………………………………………………(6分)
(2)四边形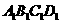 的面积为12;四边形
的面积为12;四边形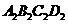 的面积为6;…………………(8分)
的面积为6;…………………(8分)
(3)四边形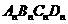 的面积为
的面积为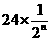 ;……………………………………………(10分)
;……………………………………………(10分)
(4)方法一:由(1)得矩形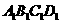 的长为4,宽为3;
的长为4,宽为3;
∵矩形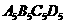 ∽矩形
∽矩形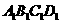 ;∴可设矩形
;∴可设矩形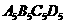 的长为4x,宽为3x,则
的长为4x,宽为3x,则
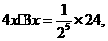 …………………………………………………………………………(12分)
…………………………………………………………………………(12分)
解得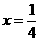 ;∴
;∴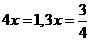 ;…………………………………………………………(13分)
;…………………………………………………………(13分)
∴矩形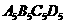 的周长=
的周长=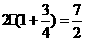 .………………………………………………(14分)
.………………………………………………(14分)
方法二:矩形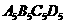 的面积/矩形
的面积/矩形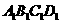 的面积
的面积
=(矩形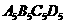 的周长)2/(矩形
的周长)2/(矩形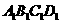 的周长)2
的周长)2
即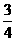 ∶12 =(矩形
∶12 =(矩形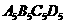 的周长)2∶142
的周长)2∶142
∴矩形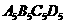 的周长=
的周长=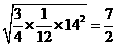
24.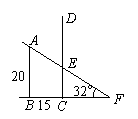
 (1)如图设CE=x米,则AF=(20
(1)如图设CE=x米,则AF=(20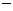 x)米……………(1分)
x)米……………(1分)
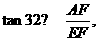 即20
即20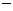 x=
x=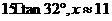 ………(4分)
………(4分)
∵11>6, ∴居民住房的采光有影响.(5分)
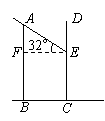
(2)如图: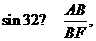
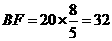 …(8分)
…(8分)
两楼应相距32米…………………………………………(9分)
23.是等腰梯形……………………………………………………………………………………(1分)
已知:梯形ABCD,AD∥BC且∠B=∠C(或∠A=∠D)………………………………(2分)
求证:梯形ABCD是等腰梯形……………………………………………………………(3分)
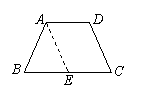 证明一:过点A作AE∥DC,交BC于E…………………………(4分)
证明一:过点A作AE∥DC,交BC于E…………………………(4分)
∵AD∥BC AE∥DC
∴四边形AECD是平行四边形,∴∠AEB=∠C,
AE=DC…………………………………………………(5分)
∵∠B=∠C
∴∠AEB=∠B………………………………………………………………………(6分)
∴AB=AE……………………………………………………………………………(7分)
∴AB=DC
 ∴梯形ABCD是等腰梯形………………………………………………………(8分)
∴梯形ABCD是等腰梯形………………………………………………………(8分)
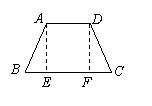
证明二:过A、D两点分别作AE⊥BC,DF⊥BC垂足为E、F
∵AE⊥BC、DF⊥BC
∴AE∥DF且∠AEB=∠DFC
 ∵AD∥BC
∵AD∥BC
∴四边形AEFD是平行四边形 ∴AE=DF
∵∠AEB=∠DFC ∠B=∠C
∴△AEB≌△DFC ∴AB=DC
∴梯形ABCD是等腰梯形
证明三:延长BA、CD交于E点
∵∠B=∠C ∴BE=CE
∴AD∥BC ∴∠EAD=∠B,∠EDA=∠C ∴∠EAD=∠EDA
∴AE=DE ∴AB=DC
∴梯形ABCD是等腰梯形
22.(1)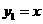 (2分) (2)
(2分) (2)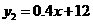 ………………………………………(4分)
………………………………………(4分)
(3) 当x>20时,选择会员卡方式合算
当x=20时,两种方式一样
当x<20时,选择零星租碟方式合算…………………………………………………(8分)
21.(1)利用计算器模拟产生随机数与这批产品编号相对应,产生10个号码即可. ………(3分)
(2)利用摸球游戏或抽签等.…………………………………………………………………(6分)
20.(1)左视图有以下5种情形(只要画对一种即给5分):

(2)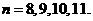 …………………………………………………………………………(9分)
…………………………………………………………………………(9分)
19.(1)将N(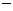 1,
1,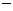 4)代入
4)代入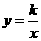 中 得k=4……………………………………………(2分)
中 得k=4……………………………………………(2分)
反比例函数的解析式为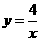 ………………………………………………………………(3分)
………………………………………………………………(3分)
将M(2,m)代入解析式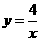 中 得m=2…………………………………………(4分)
中 得m=2…………………………………………(4分)
将M(2,2),N(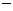 1,
1,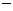 4)代入
4)代入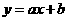 中
中
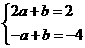 解得a=2 b=-2……………………………………………………(7分)
解得a=2 b=-2……………………………………………………(7分)
一次函数的解析式为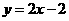 ……………………………………………………………(8分)
……………………………………………………………(8分)
(2)由图象可知:当x<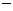 1或0<x<2时反比例函数的值大于一次函数的值.………(12分)
1或0<x<2时反比例函数的值大于一次函数的值.………(12分)
18.(1)1997年至2003年甲校学生参加课外活动的人数比乙校增长的快……………………(3分)
(学生给出其它答案,只要正确、合理均给3分)
(2)甲校学生参加文体活动的人数比参加科技活动的人数多;……………………………(6分)
(学生给出其它答案,只要正确、合理均给3分)
(3)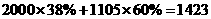 ……………………………………………………(9分)
……………………………………………………(9分)
答:2003年两所中学的学生参加科技活动的总人数是1423人.…………………………(10分)
17.原式=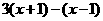 ……………………………………………………………………(4分)
……………………………………………………………………(4分)
=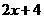 ……(5分)当
……(5分)当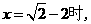 原式=
原式=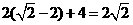 ……………(8分)
……………(8分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com