5.　 小兰和小潭分别用掷A、B两枚骰子的方法来确定P(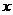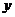，)的位置，她们规定：小兰掷得的点数为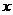，小谭掷得的点数为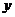，那么，她们各掷一次所确定的点落在已知直线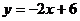上的概率为(　　　 )

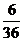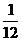　A、　　　　　 B、　　　　　 C、　　　　　 D、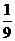

4. 如图，正方形硬纸片ABCD的边长是4，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是(　　　 )。

(A)2　 (B)4　 (C)8　 (D)10

3. 设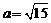，则实数a在数轴上对应的点的大致位置是(　　　 )。

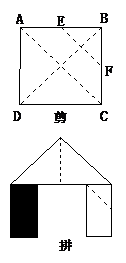
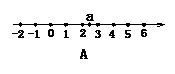
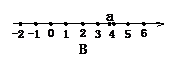
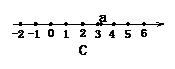
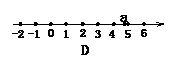
2. 下列计算不正确的是(　 )

A.(a－1)(－1－a)＝1－a²　　　 B. a³+2 a³＝3 a³　

C.(a+1)²＝a²+1　　　　　　 　　D.(－a³)²÷a²＝a⁴

1.函数y=自变量x的取值范围是(　 )

　 A．x＞0　　　　　　 B．x＜0　　　　 C．x=0　　　　　 D．x≠0

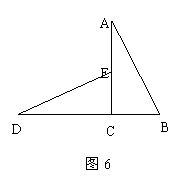
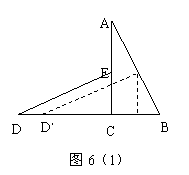
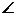25.如图6：ACB与DCE是全等的两个直角三角形，其中ACB=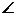DCE=90⁰，AC=4，BC=2，点D、C、B在同一条直线上，点E在边AC上.

(1)直线DE与AB有怎样的位置关系？请证明你的结论；

(2)如图6(1)若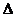DCE沿着直线DB向右平移多少距离时，点E恰好落在边AB上，求平移距离DD^，；

(3)在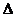DCE沿着直线DB向右平移的过程中，使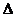DCE与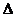ACB的公共部分是四边形，设平移过程中的平移距离为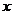，这个四边形的面积为，求与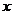的函数关系式，并写出它的定义域.

24.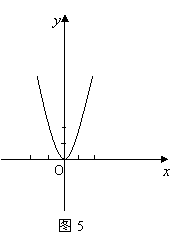将二次函数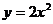(如图5)向右平移1个单位所得的二次函数的图象的顶点为点D，并与轴交于点A.

　 (1)写出平移后的二次函数的对称轴与点A的坐标；

　(2)设平移后的二次函数的对称轴与函数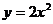的交点为点B，

试判断四边形OABD是什么四边形？请证明你的结论；

　 (3)能否在函数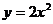 的图象上找一点P，

使DBP是以线段DB为直角边的直角三角形？

若能，请求出点P的坐标；若不能，请简要说明理由.

23.如图4：AB是⊙O的直径，点P是AB延长线上一点，PD是⊙O的切线，切点为点D，连结OD，点C是⊙O上一点，且PC=PD.

　 (1)求证：直线PC是⊙O的切线；

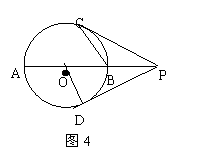　 (2)连结BC，CB=BP，PD=，求⊙O的半径.

22.已知关于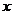的方程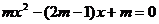有两个不相等的实数根.

(1)求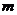的取值范围；(2)当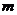取最大整数时，求方程的两个根.

21.如图3：在Rt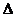ACB中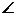，C=90⁰，AC=8，BC=6，CD是斜边AB上的高.

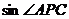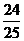　 若点P在线段DB上，连结CP，=.求CP的长.