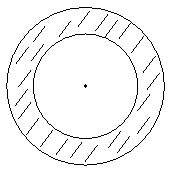
6．(内江市 10分)小红和小明在操场做游戏，他们先在地上画了半径分别2m和3m的同心圆(如图)，蒙上眼在一定距离外向圈内掷小石子，掷中阴影小红胜，否则小明胜，未掷入圈内不算，你来当裁判。

⑴你认为游戏公平吗？为什么？

⑵游戏结束，小明边走边想，“反过来，能否用频率估计概率的方法，来估算非规则图形的面积呢？”。请你设计方案，解决这一问题。(要求画出图形，说明设计步骤、原理，写出公式)

4。(泰山 10分)如图，AB切⊙O于点B，OA交⊙O于C点，过C作DC⊥OA交AB于D，且BD：AD=1：2

(1)求∠A的正切值.(4分)

(2)若OC =1，求AB及 BC的长.(6分)

5(河北10分) 某食品零售店为仪器厂代销一种面包，未售出的面包可退回厂家，以统计销售情况发现，当这种面包的单价定为7角时，每天卖出160个。在此基础上，这种面包的单价每提高1角时，该零售店每天就会少卖出20个。考虑了所有因素后该零售店每个面包的成本是5角。

设这种面包的单价为x(角)，零售店每天销售这种面包所获得的利润为y(角)。

⑴用含x的代数式分别表示出每个面包的利润与每天卖出的面包个数；

每个面包的利润为　　　 　　角，每天卖出的面包个数为　　　　　　　　

⑵求y与x之间的函数关系式；

⑶当面包单价定为多少时，该零售店每天销售这种面包获得的利润最大？最大利润为多少？

3. 山东省青岛市(本小题满分10分)

在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下方案(如图①所示)：

(1)在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE=α;

(2)量出测点A到旗杆底部N的水平距离AN=;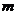

(3)量出测倾器的高度AC=.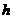

根据上述测量数据，即可求出旗杆的高度MN.

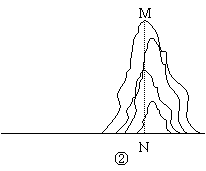
如果测量工具不变，请仿照上述过程，设计一个测量某小山高度(如图②)的方案：

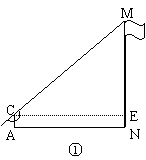(1)在图②中，画出你测量小山高度MN的示意图(标上适当字母)； 　(2)写出你设计的方案.

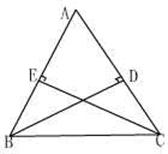
1．(十堰市)(8分)

如图:已知△ABC中，BD.CE是△ABC的高。请你增加一个条件，写出一个结论，并证明你写出的结论。

增加的条件为：

已知：

求证：

证明:

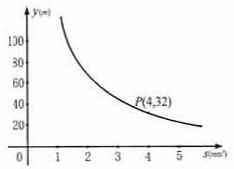
2(济南市8分)、你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细(横截面积)s(mm²)的反比例函数，其图象如图所示。

⑴写出y与s的函数关系式；

⑵求当面条粗1.6mm²时，面条的总长度是多少米？

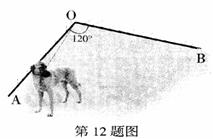
8．(宁德)如图，墙OA、OB的夹角ÐAOB＝120º，OA=7m。OB=9m，一根9m长的绳子一端栓在墙角

O处，另一端栓着一只小狗，则小狗可活动的区域的面积是 　　　　　　　　m²(结果保留π)。

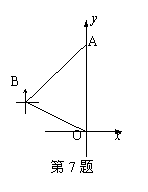
7. (泰州市) 如图，机器人从A点沿着西南方向，行了4个单位，到达B点后观察到原点O在它的南偏东60°的方向上，则原来A的坐标为　　　　　

(结果保留根号)．

6．如图10，在⊙O中，已知∠ACB=∠CDB=60°，AC=3，则⊙O的半径是　　　　　　　 ．

4．(广东茂名)用一个平面去截一个正方体其截面形状不可能的

是 　　　　　　　　　　　　　　　　　　　　　(请你在三角形、四边形、五边形、六边形、七边形这五种图择符合题意的图形填上即可)；

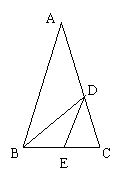
5(嘉兴)顶角为36°的等腰三角形称为黄金三角形，如 图，△ABC、△BDC、

△DEC都是黄金三角,已知AB=1，则DE=___________________

3.(江西)收音机刻度盘的波长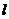和频率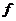分别是用米(m)和千赫兹(kHz)为单位标刻的。波长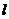和频率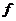满足关系式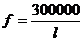，这说明波长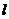越大，频率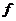就越_________　　 ；

2.(泰山)在边长为3㎝、4㎝、5㎝的三角形白铁皮上剪下一个最大的圆，此圆的半径为____　　 　　㎝.