
题目列表(包括答案和解析)
21.解:(1)由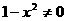 ,得
,得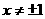 ,所以函数
,所以函数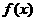 的定义域为
的定义域为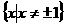 .
.
(2)易知,函数的定义域关于原点对称,又
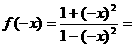
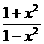 =
=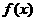 , 所以函数
, 所以函数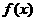 为偶函数.
为偶函数.
(3)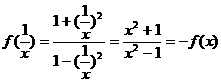
(4)证明:设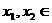
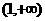 ,且
,且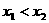 ,则
,则
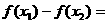
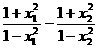
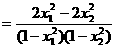
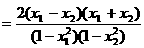
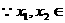
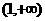 ,且
,且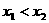 ,
,
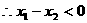 ,
,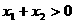 ,
,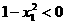 ,
,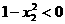 ,
,
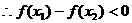 ,即
,即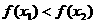
故函数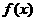 在区间
在区间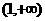 上是增函数.
上是增函数.
19.解:设1<x1<x2, f (x2)-f (x1
)=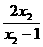 --
--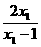 =
=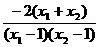
因为1< x1<x2,,所以x1+ x1 >0, x1-1>0, x2 -1>0,
所以f (x2)-f (x1 )-f (x1 )<0, 即f (x2)<f (x1 )
所以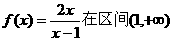 是单调减函数。
是单调减函数。
 20.解:
20.解: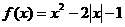
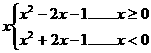
图(略)
单调增区间为(-1,0),(1,+∞),
单调减区间为(-∞,-1),(0,1)
18.解:⑴A∩B=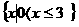 ,A∪B=
,A∪B=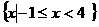 ………8
………8
⑵a≥4…………………………………………………14
17.解:(CUA)∩(CUB)={x|-1<x<1}
13._20_ 14. -2 15. _6_ 16. _4_
1. D 2.B 3.B 4.C 6.A 7. B 8.C 9.C 10.D 11. C 12. A
22.某城市出租车,乘客上车后,行驶3km内收费都是10元,之后每行驶1km收费2元,超过15km,每行驶1km收费为3元(假设途中一路顺利,没有停车等候,).若乘客需要行驶20km,求
(1) 付费总数y与行驶路程x收费之间的函数关系式;
(2) 当出租车行驶了15km后,乘客是中途换乘一辆出租车还是继续乘坐这辆出租车行驶完余下的5km路程,哪一种方式更便宜?
21.设函数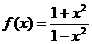 .
.
(1)求它的定义域; (2) 判断它的奇偶性; (3) 求证: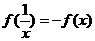 ;
;
(4)证明:函数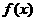 在区间
在区间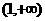 上是增函数.
上是增函数.
19. 试用定义判断函数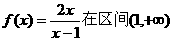 上的单调性.
上的单调性.
 20 将函数
20 将函数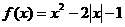 写成分段函数的形式,并在坐标系中作出他的图像,然后写出该函数的单调区间。
写成分段函数的形式,并在坐标系中作出他的图像,然后写出该函数的单调区间。
18. 设全集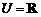 ,集合
,集合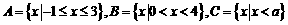 。
。
(1)求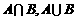 ;
;
(2)若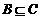 ,求实数
,求实数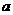 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com