
题目列表(包括答案和解析)
22.解:(1)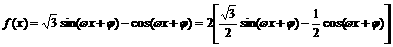
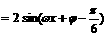 ………………………………………………………2分
………………………………………………………2分
因为 为偶函数,所以对
为偶函数,所以对 ,
,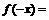
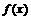 恒成立,
恒成立,
所以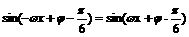
即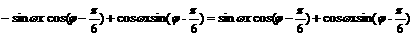
整理得: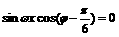 ……………………………………………………4分
……………………………………………………4分
∵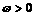 ,且
,且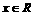 ,∴
,∴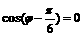
又∵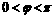 ,故
,故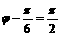 ,∴
,∴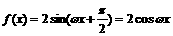
由题意得: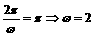 ,∴
,∴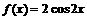 ,
,
从而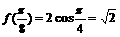 …………………………………………………………6分
…………………………………………………………6分
(2)将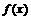 的图象向右平移
的图象向右平移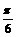 个单位后,得到
个单位后,得到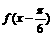 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到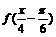 的图象,
的图象,
所以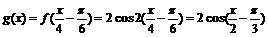 ……………………………8分
……………………………8分
由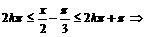
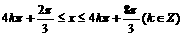
因此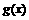 的单调递减区间为:
的单调递减区间为: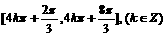 ……………………10分
……………………10分
22.(本小题10分)已知函数 为偶函数,且函数 y=f (x) 图象的两相邻对称轴间的距离为
为偶函数,且函数 y=f (x) 图象的两相邻对称轴间的距离为 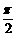 .
.
(1)求 f (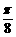 ) 的值;
) 的值;
(2)将函数 y = f (x) 的图象向右平移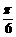 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y = g (x) 的图象,求
g (x) 的单调递减区间
.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y = g (x) 的图象,求
g (x) 的单调递减区间
.
21.解:(1)由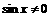 得函数
得函数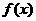 的定义域为
的定义域为 …………………………3分
…………………………3分
(2)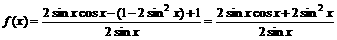
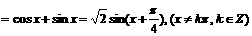 ………………4分
………………4分
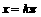 时,
时,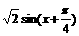 的值为1或-1,又由于
的值为1或-1,又由于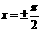 时,
时,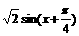 的值为1或-1,
的值为1或-1,
所以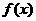 的值域为:
的值域为: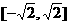 …………………………………………6分
…………………………………………6分
(3)令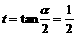 ,得
,得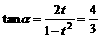 ……………………………………8分
……………………………………8分
由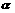 为锐角,得
为锐角,得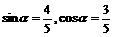 ……………………………………………………9分
……………………………………………………9分
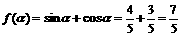 …………………………………………………………10分
…………………………………………………………10分
21.(本小题10分)已知函数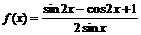 .
.
(1)求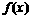 的定义域;
的定义域;
(2)求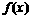 的值域;
的值域;
(3)设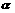 为锐角,且
为锐角,且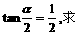
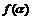 的值.
的值.
20.解:∵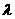
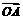 -
-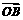 =(
=(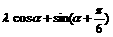 ,
,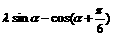 )……………………2分
)……………………2分
∴|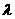
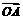 -
-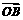 |=
|=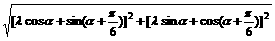
=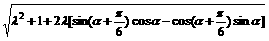
=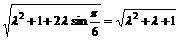 ……………………………………4分
……………………………………4分
由已知得:|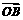 |=1 ……………………………………………………………………6分
|=1 ……………………………………………………………………6分
又∵|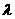
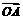 -
-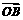 |≥
|≥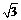 |
|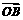 |,∴
|,∴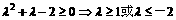 ……………………………8分
……………………………8分
20.(本小题8分)已知向量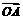 =(cosα,sinα),
=(cosα,sinα), 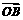 =(-sin(α+
=(-sin(α+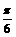 ),cos(α+
),cos(α+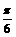 )),其中O为原点,实数
)),其中O为原点,实数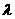 满足|
满足|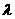
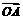 -
-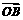 |≥
|≥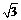 |
|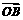 |,求实数
|,求实数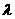 的取值范围.
的取值范围.
19.解:由sin(α-β)=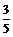 及α-β∈(
及α-β∈(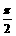 ,π)得:cos(α-β)=
,π)得:cos(α-β)= 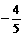 ,……………………………………2分
,……………………………………2分
由sin(α+β)=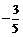 及α+β∈(
及α+β∈(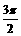 ,2π)得:cos(α+β)=
,2π)得:cos(α+β)= 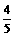 ………………………………4分
………………………………4分
cos2β=cos[(α+β)-(α-β)]=cos(α+β)cos(α-β)+sin(α+β)sin(α-β) ………………………6分
=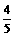 ×(
×(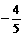 )+(
)+(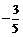 )×
)×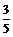 =-1……………………………………………………8分
=-1……………………………………………………8分
19.(本小题8分)已知sin(α-β)=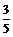 ,sin(α+β)=
,sin(α+β)=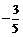 ,且α-β∈(
,且α-β∈(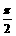 ,π), α+β∈(
,π), α+β∈(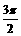 ,2π),求cos2β的值.
,2π),求cos2β的值.
18.解:作CD∥OB交直线OA于点D,作CE∥OA交直线OB于点E
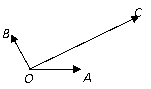 则
则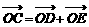 ………………………………………………3分
………………………………………………3分
由已知∠OCD=∠COE=120º-30º=90º
在Rt△OCD中,OD=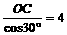
CD=OCtan30º=2,∴OE=CD=2 …………………………6分
又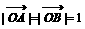 ,∴
,∴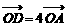 ,
,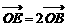
从而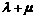 =6……………………………………………………8分
=6……………………………………………………8分
18.(本小题8分)如图,平面内有三个向量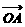 ,
,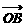 ,
,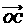 ,其中
,其中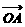 与
与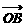 的夹角为
的夹角为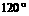 ,
, 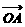 与
与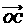 的夹角为30°,且|
的夹角为30°,且|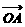 |=|
|=|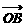 |= 1,|
|= 1,|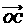 |=2.若
|=2.若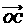 =
=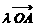 +
+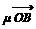
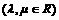 ,求
,求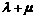 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com