
题目列表(包括答案和解析)
2.函数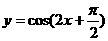 的图象的一条对称轴方程是( )
的图象的一条对称轴方程是( )
A.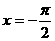 B.
B. 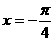 C.
C.
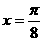 D.
D.
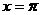
1.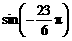 的值等于
( )
的值等于
( )
A. 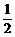 B.
B.
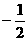 C.
C.
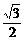 D.
D.
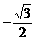
17(本小题满分8分)
(1)已知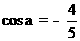 ,且
,且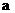 为第三象限角,求
为第三象限角,求 的值
的值
(2)已知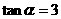 ,计算
,计算 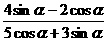 的值
的值
18(本小题满分8分)
已知向量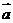 ,
, 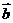 的夹角为
的夹角为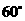 , 且
, 且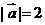 ,
, 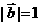 ,
,
(1) 求 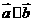 ;
(2) 求
;
(2) 求 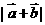 .
.
19.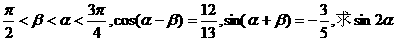 (满分8分)已知
的值.
(满分8分)已知
的值.
20(本小题满分8分)
已知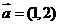 ,
,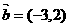 ,当
,当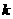 为何值时,
为何值时,
(1) 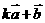 与
与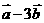 垂直?
垂直?
(2) 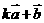 与
与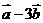 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
21(本小题满分10分)
某港口的水深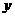 (米)是时间
(米)是时间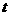 (
(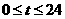 ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
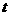 ] ] |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24[ |
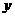 |
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测, 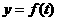 可近似的看成是函数
可近似的看成是函数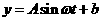
(1)根据以上数据,求出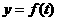 的解析式
的解析式
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
22(本小题满分10分)
已知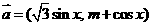 ,
,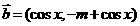 , 且
, 且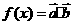
(1) 求函数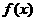 的解析式;
的解析式;
(2) 当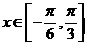 时,
时, 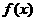 的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数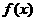 的最大值, 并求出相应的
的最大值, 并求出相应的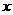 的值.
的值.

 19:解:(8分)由题设知
19:解:(8分)由题设知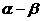 为第一象限的角。
为第一象限的角。
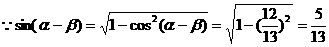 (2分)
(2分)
由题设知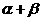 为第二象限的角,
为第二象限的角,
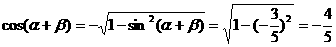 (4分)
(4分)
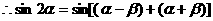
=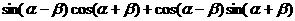 -----(6分)
-----(6分)
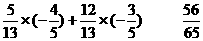
= =- --(8分)
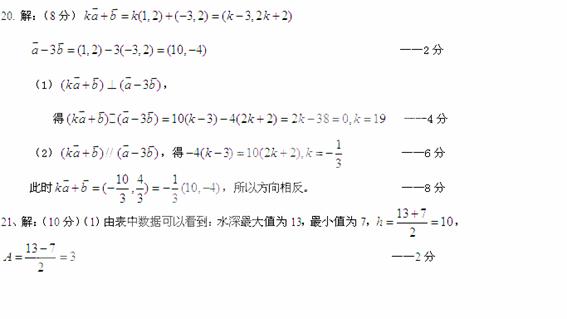 且相隔9小时达到一次最大值说明周期为9,因此
且相隔9小时达到一次最大值说明周期为9,因此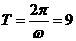 ,
,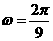 ,
,
故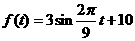
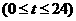 --4分
--4分
(2)要想船舶安全,必须深度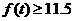 ,即
,即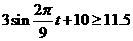 --6分
--6分
∴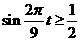
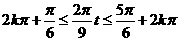 解得:
解得: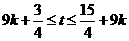
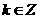 --8分
--8分
又 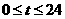
当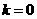 时,
时,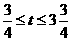 ;当
;当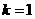 时,
时,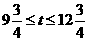 ;当
;当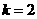 时,
时,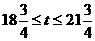
故船舶安全进港的时间段为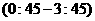 ,
,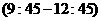 ,
,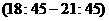 -10分
-10分
22解:(10分) (1) 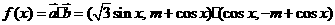
即 --4分
--4分
(2) 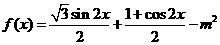
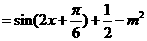 --6分
--6分
由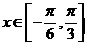 ,
, 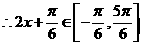 ,
, 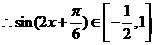 ,
,
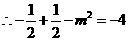 ,
, 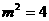

 --8分[
--8分[
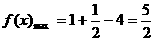 , 此时
, 此时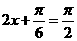 ,
, 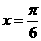 . --10分
. --10分
16. 给出下列五个命题:
①函数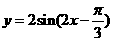 的一条对称轴是
的一条对称轴是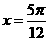 ;
;
②函数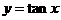 的图象关于点(
的图象关于点(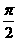 ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数
④若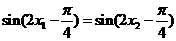 ,则
,则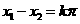 ,其中
,其中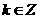
以上四个命题中正确的有 1 4 (填写正确命题前面的序号)
15.已知 tan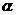 =2,则sin
=2,则sin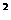
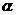 +sin
+sin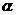 cos
cos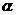 =
。
=
。
14.设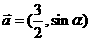 ,
,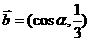 ,且
,且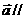
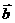 ,则锐角
,则锐角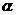 为
。
为
。
13.已知扇形的圆心角为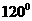 ,半径为
,半径为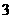 ,则扇形的面积是 。
,则扇形的面积是 。
12.平面直角坐标系中,已知两点A(3,1),B(-1,3),若点C满足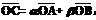
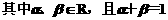 ,则点C的轨迹方程是( )
,则点C的轨迹方程是( )
A.3x+2y-11=0; B.(x-1)2+(y-2)2=5;
C.2x-y=0; D.x+2y-5=0;
|
二 |
17] |
18 |
19 |
20 |
21 |
22 |
总分 |
|
|
|
|
|
|
|
|
|
第II卷(非选择题, 共64分)
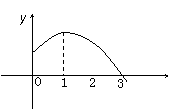
11.函数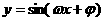 的部分图象如右图,则
的部分图象如右图,则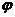 、
、 可以取的一组值是( )
可以取的一组值是( )
 A.
A. 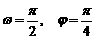
B. 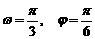
C. 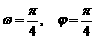
D. 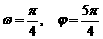
10.已知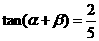 ,
, 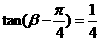 , 则
, 则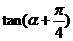 的值为( )
的值为( )
A 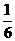 B
B
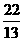 C
C
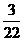 D
D
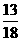
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com