
题目列表(包括答案和解析)
1.看下面的四段话,其中不是解决问题的算法的是 ( )
A.从济南到北京旅游,先坐火车,再坐飞机抵达
B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1
C.方程x2-1=0有两个实根
D.求1+2+3+4+5的值,先计算1+2=3,再由于3+3=6,6+4=10,10+5=15,最终结果为15
22. (本题满分14分)
已知定义在区间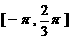 上的函数
上的函数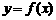 的图象关于直线
的图象关于直线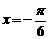 对称,
对称,
 当
当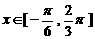 时,函数
时,函数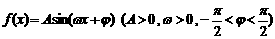 ,其图象如图所示.
,其图象如图所示.
(Ⅰ) 求函数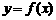 在
在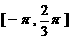 的表达式;
的表达式;
(Ⅱ) 求方程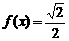 的解.
的解.
(Ⅲ)是否存在常数 的值,使得
的值,使得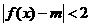 在
在
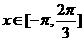 上恒成立;若存在,求出
上恒成立;若存在,求出 的取
的取
值范围;若不存在,请说明理由.
解:(Ⅰ)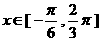 ,
,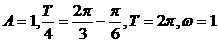
且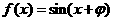 过
过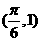 ,∵
,∵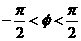
∴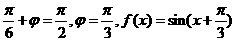 ……2分
……2分
当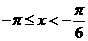 时,
时,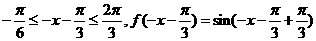
而函数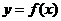 的图象关于直线
的图象关于直线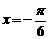 对称,则
对称,则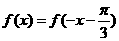
即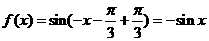 ,
,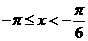
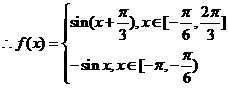 ……5分
……5分
(Ⅱ)当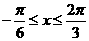 时,
时,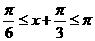 ,
,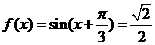
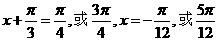 ……8分
……8分
当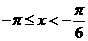 时,
时,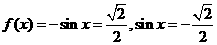
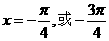
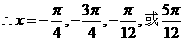 为所求
为所求 ……10分
……10分
(Ⅲ)由条件得: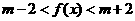 在
在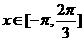 上恒成立K^S*5U.C#O%
上恒成立K^S*5U.C#O%
即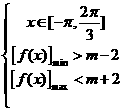 ,由图象可得:
,由图象可得: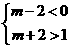
∴ 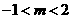 ……14分
……14分
21. (本题满分12分)
已知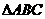 中,
中,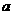 、
、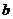 、
、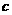 分别是三个内角
分别是三个内角 、
、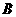 、
、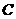 的对边,关于
的对边,关于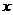 的不等式
的不等式 的解集是空集.
的解集是空集.
(Ⅰ)求角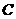 的最大值;
的最大值;
(Ⅱ)若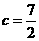 ,
,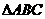 的面积
的面积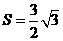 ,求当角
,求当角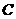 取最大值时
取最大值时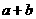 的值.
的值.
解:(Ⅰ)∵不等式 的解集是空集。K^S*5U.C#O%
的解集是空集。K^S*5U.C#O%
∴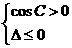 ,即
,即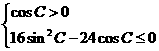 ,
,
即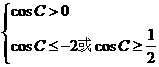 ,
……4分
,
……4分
故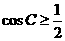 ,∴角
,∴角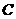 的最大值为
的最大值为 。
……6分
。
……6分
(Ⅱ)当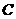 =
= 时,
时,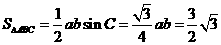 ,∴
,∴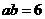 ,……8分
,……8分
由余弦定理得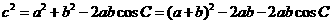 , ……10分
, ……10分
∴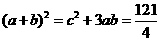 ,∴
,∴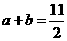 。
……12分
。
……12分
20. (本题满分12分)
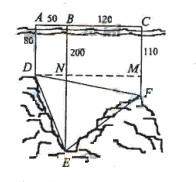
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知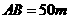 ,
, 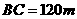 ,于A处测得水深
,于A处测得水深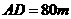 ,于B处测得水深
,于B处测得水深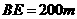 ,于C处测得水深
,于C处测得水深 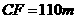 ,求∠DEF的余弦值。
,求∠DEF的余弦值。
 解:作
解:作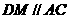 交BE于N,交CF于M.K^S*5U.C#O%
交BE于N,交CF于M.K^S*5U.C#O% 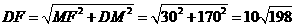 ,
,
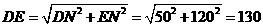
 ,
,
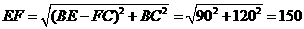 .
.
在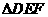 中,由余弦定理,
中,由余弦定理,
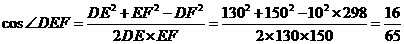
19. (本题满分12分)
已知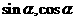 是方程
是方程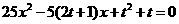 的两根且
的两根且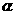 为锐角,求t的值。K^S*5U.C#O%
为锐角,求t的值。K^S*5U.C#O%
解:由韦达定理得 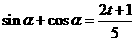 ,
,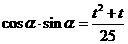 ……4分
……4分
∵α为锐角 ∴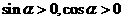 , 则
, 则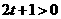 且
且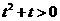 得t>0 ……8分
得t>0 ……8分
则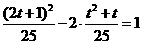 解之得:t=3或t=-4(舍去),
∴t=3
……12分
解之得:t=3或t=-4(舍去),
∴t=3
……12分
18. (本题满分12分)
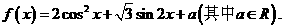 已知:K^S*5U.C#O%
已知:K^S*5U.C#O%
(Ⅰ)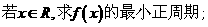
(Ⅱ)
解: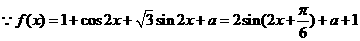 ……3分
……3分
(Ⅰ)最小正周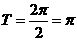 ……6分
……6分
(Ⅱ)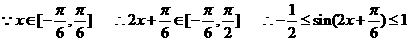 ……9分
……9分
即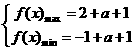
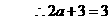 即:
即: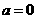 ……12分
……12分
17. (本题满分12分)
已知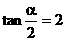 , 求: (Ⅰ)
, 求: (Ⅰ)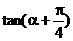 的值; (Ⅱ)
的值; (Ⅱ)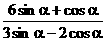 的值。
的值。
解:(Ⅰ) ∵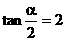 , ∴
, ∴ 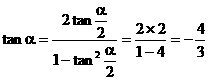 ; ……4分
; ……4分
所以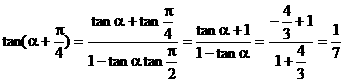 . ……8分
. ……8分
(Ⅱ)由(1)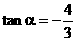 , 所以
, 所以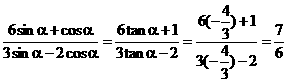 ……12分
……12分
13、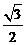 14、
14、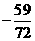 15、
15、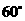 16、③④
16、③④
1~6: CABCDB 7~12: BBACCD
22. (本题满分14分)
 已知定义在区间
已知定义在区间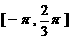 上的函数
上的函数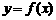 的图象关于直线
的图象关于直线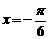 对称,当
对称,当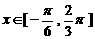 时,函数
时,函数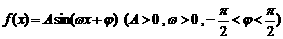 ,其图象如图所示
,其图象如图所示
(Ⅰ)求函数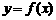 在
在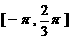 的表达式;
的表达式;
(Ⅱ)求方程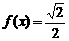 的解。
的解。
(Ⅲ)是否存在常数 的值,使得
的值,使得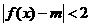 在
在
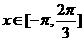 上恒成立;若存在,求出
上恒成立;若存在,求出 的取
的取
值范围;若不存在,请说明理由。
南安一中2009-2010学年高一(下)期中考试数学试卷
(答案)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com