
题目列表(包括答案和解析)
2.函数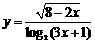 的定义域是( )
的定义域是( )
A.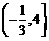 B.
B.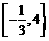 C.
C.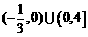 D.
D.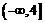
1.集合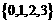 的含有元素1的真子集共有( )个
的含有元素1的真子集共有( )个
A.4 B.6 C.7 D.8
20.解:(1)规定 f(0)= 1.
表示没有用水清洗时,手上的残留污物没有发生变化. ……………… 1分
(2)f(x)应该有f(0)= 1,f(1)=,
且在[0,+∞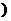 上,f(x)是单调递减的,
上,f(x)是单调递减的,
∴ f(x)的定义域是[0,+∞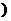 ,值域为(0,1
,值域为(0,1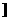 . ……………… 3分
. ……………… 3分
(3)设清洗前污物的残留量为1,
那么用a单位量的清水清洗一次后,残留的污物量为:
W1 = 1×f(a)= . ……………… 4分
如果采用后一方案:每次用的清水清洗:高☆考♂资♀源?网 ☆
清洗第一次后:残留的污物量为:1×f()==;
清洗第二次后:残留的污物量为:W2=×f()=. ……………… 6分
∵ W1-W2 = -=>0, ……………… 9分
∴ W1>W2,
即采用将水平均分成两份后清洗两次,残留的污物量比较少. ……………… 10分
w.w.^w.k.s.5*
19.解:(1)由题意,函数f(x)是g(x)的反函数.高☆考♂资♀源?网 ☆
设y =+1,则y-1=,∴ x =(y-1)2-2, ……………… 2分
∵ x≥-2,∴ y≥1,
∴ f(x)=(x-1)2-2 = x2-2x-1,x∈[1,+∞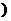 .
……………… 4分
.
……………… 4分
(2)函数f(x)在其定义域x∈[1,+∞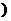 内是增函数. ……………… 6分
内是增函数. ……………… 6分
设1≤x1<x2,
则 f(x1)-f(x2)=(x1-1)2-2-(x2-1)2 + 2
=(x1-x2)(x1 + x2-2). ……………… 8分
∵ 1≤x1<x2,则 x1-x2<0,而x1 + x2>2,∴ x1 + x2-2>0,
∴ f(x1)-f(x2)=(x1-x2)(x1 + x2-2)<0,
即 f(x1)<f(x2).
∴ f(x)在[1,+∞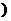 上是单调增函数.
……………… 10分
上是单调增函数.
……………… 10分
18.解:(1)∵ {an}是等差数列,∴ an = an + b(或者用an = a1 +(n-1)d).高☆考♂资♀源?网 ☆
∴ a4 = 4a + b = 7,a10 = 10a + b = 19.
∴ a = 2,b =-1,即an = 2n-1. ……………… 3分
(2)∵ bn= 2n,∴ ==2(n≥2),
且 b1 = 21 = 2,
∴ {bn}是以2为首项,2为公比的等比数列. ……………… 6分
(3)∵ cn = an + 2bn = 2n-1 + 2n+1,
∴ Sn = 2×1-1 + 22 + 2×2-1 + 23 + … + 2n-1 + 2n+1高☆考♂资♀源?网 ☆
= 2(1 + 2 + … + n)-n + 22(1 + 2 + 22 + … + 2n-1) ……………… 8分
= n2 + 22(2n-1)
= 2n+2-4 + n2. ……………… 10分
17.解:∵ A ={ x︱(x + 1)(x-3)≥0 } =(-∞,-1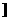 ∪[ 3,+∞
∪[ 3,+∞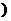 ………… 2分
………… 2分
∴ 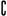 RA =(-1,3).
……………… 4分
RA =(-1,3).
……………… 4分
B ={ x︱1->0,a>0} = { x︱>0,a>0}
= { x︱x<-a或x>a,a>0}. ……………… 6分
∴(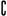 RA)∩ B = Æ Û ……………… 8分
RA)∩ B = Æ Û ……………… 8分
Û Û a≥3. ……………… 10分
13.{x︱-3<x<3} 14.(0, 15.15 lg 2 16.②④
15.15 lg 2 16.②④
1-5 ADBBD 6-10 AABCD 11-12 BC
20.在日常生活中,我们经常需要用清水来洗手,特别是在目前甲流期间,我们更要注意个人清洁卫生.现在我们对用一定量的清水洗一次手的效果作如下假定:用1个单位量的清水可以清洗掉手上污物量的50%,用水越多,洗掉的污物量也越多,但总还是有污物残留在手上.设用x单位量的清水洗一次后,手上残留的污物量与本次清洗前残留的污物量之比为函数f(x).
(1)试规定f(0)的值;高☆考♂资♀源?网 ☆
(2)试根据假定写出f(x)的定义域和值域(可以不说明理由);
(3)设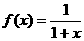 ,现只有a(a>0)单位量的清水,可以清洗一次,也可以将水平均分成两份后清洗两次.试问选用哪种方式清洗后手上残留的污物量比较少?请说明理由.
,现只有a(a>0)单位量的清水,可以清洗一次,也可以将水平均分成两份后清洗两次.试问选用哪种方式清洗后手上残留的污物量比较少?请说明理由.
高中2012级第一学期末教学质量测试
 数学参考答案及评分意见
数学参考答案及评分意见
19.已知函数f(x)的图象与函数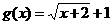 (x≥-2)的图象关于直线y = x对称.
(x≥-2)的图象关于直线y = x对称.
 (1)求f(x)的解析式;
(1)求f(x)的解析式;
(2)试判断f(x)在其定义域上的单调性,并用定义证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com