2.计算__　 ▲　 __.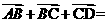

1. 计算__　 ▲　 __.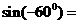

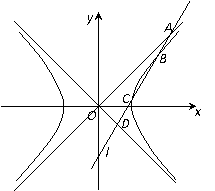
20. 已知双曲线M：x²－y²=1，直线l与双曲线M的实轴不垂直，且依次交直线y=x、双曲线M、直线y=－x于A、B、C、D 四点，O为坐标原点．

(1) 若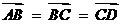，求△AOD的面积；

(2) 若△BOC的面积等于△AOD面积的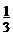，求证：．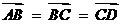

19.(本小题满分16分)

平面直角坐标系xOy中，已知⊙M经过点F₁(0，－c)，F₂(0，c)，A(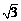c，0)三点，其中c＞0．

(1)求⊙M的标准方程(用含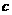的式子表示)；

(2)已知椭圆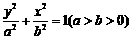(其中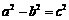)的左、右顶点分别为D、B，

⊙M与x轴的两个交点分别为A、C，且A点在B点右侧，C点在D点右侧．

①求椭圆离心率的取值范围；

②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上，问直线MF₁与直线DF₂的交点是否在一条定直线上？若是，请求出这条定直线的方程；若不是，请说明理由．

18. 设O为坐标原点，曲线x²+y²+2x－6y+1=0上有两点P、Q，满足关于直线x+my+4=0对称，又满足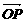·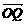=0.

(1)求m的值；(2)求直线PQ的方程.

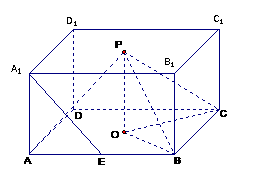
17.如图，O，P分别是正四棱柱ABCD－A₁B₁C₁D₁底面中心，E是AB的中点，AB=kAA₁，

　　 (1)求证：A₁E∥平面PBC；

(2)当k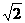＝时，求直线PA与平面PBC所成角的大小；

　　 (3) 当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？

16. (本小题满分14分)已知点P(2，－1)，求：

(1)过P点与原点距离为2的直线l的方程；w*w^w.k&s#5@

(2)过P点与原点距离最大的直线l的方程，最大距离是多少?

15. (本小题满分14分)

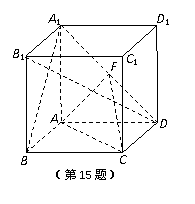正方体ABCD-A₁B₁C₁D₁中，点F为A₁D的中点．

(1)求证：A₁B∥平面AFC；

(2)求证：平面A₁B₁CD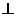平面AFC．

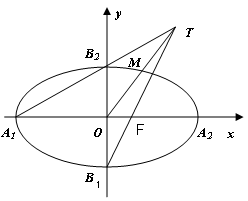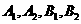14. 如图，在平面直角坐标系中，为椭圆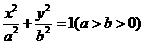的四个顶点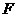，为其右焦点，直线与直线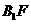相交于点T，线段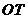与椭圆的交点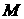恰为线段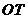的中点，则该椭圆的离心率为　　 ▲　　 　.

13. A、B是双曲线C的两个顶点，直线l与实轴垂直，与双曲线C 交于P、Q两点，若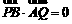，则双曲线C的离心率e＝　 ▲　 ．