
题目列表(包括答案和解析)
6.如果函数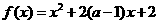 在区间
在区间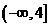 上是减少的,那么实数
上是减少的,那么实数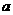 的取值范围是( )
的取值范围是( )
A
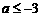 B
B 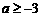 C
C 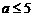 D
D 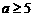
5.二次函数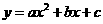 中,
中,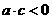 ,则函数的零点个数是(
)
,则函数的零点个数是(
)
A 0个 B 1个 C 2个 D 无法确定
4.已知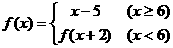 ,则f(3)为( )
,则f(3)为( )
A 2 B 3 C 4 D 5
2.下列对应关系f中,不是从集合A到集合B的映射的是( )
A
A=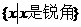 ,B=(0,1),f:求正弦; B
A=R,B=R,f:取绝对值
,B=(0,1),f:求正弦; B
A=R,B=R,f:取绝对值
C
A=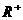 ,B=R,f:求平方; D A=R,B=R,f:取倒数
www.k@s@5@
高#考#资#源#网
,B=R,f:求平方; D A=R,B=R,f:取倒数
www.k@s@5@
高#考#资#源#网
3二次函数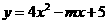 的对称轴为
的对称轴为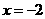 ,则当
,则当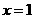 时,
时,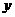 的值为 ( )
的值为 ( )
A 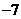 B 1
C 17
D 25
B 1
C 17
D 25
1.函数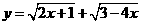 的定义域为( )
的定义域为( )
A
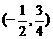 B
B 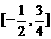 C
C 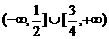 D
D 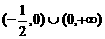
20.解:(1).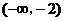 ;当
;当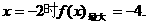 ……4分
……4分
(2).证明:设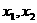 是区间,
是区间,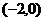 上的任意两个数,且
上的任意两个数,且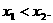
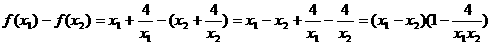
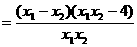
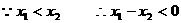
又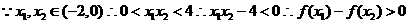
 函数在(0,2)上为减函数.
………………………11分
函数在(0,2)上为减函数.
………………………11分
(3)思考: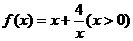
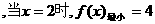 …………………………14分
…………………………14分
21(1)证明: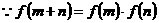 ,
,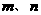 为任意实数,
为任意实数,
取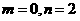 ,则有
,则有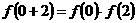
 当
当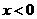 时,
时,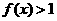 ,
,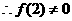 ,
,
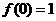 ……2分
……2分
当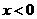 时,
时,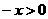
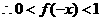 ,则
,则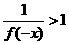
取 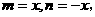 则
则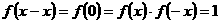
则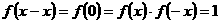
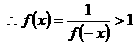 ……4分
……4分
(2)证明:由(1)及题设可知,在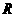 上
上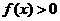
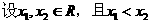 ,
,
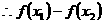
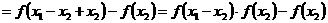
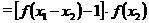 …………7分
…………7分
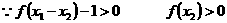

所以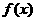 在
在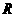 上是减函数…………8分
上是减函数…………8分
(3)解:在集合 中
中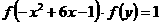
由已知条件,有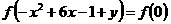
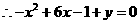 ,即
,即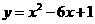 …………11分
…………11分
在集合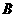 中,有
中,有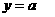

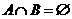 ,则抛物线
,则抛物线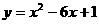 与直线
与直线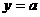 无交点
无交点

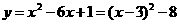 ,
,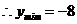 ,
,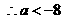
即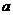 的取值范围是
的取值范围是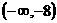 …………14分
…………14分
19.解(1)由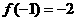 知,
知,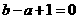 ①,又
①,又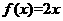 有唯一的解,故
有唯一的解,故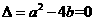 将①式代入上式得:,
将①式代入上式得:,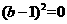 故
故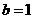 ,代入①得,
,代入①得,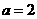 ………7分
………7分
(2)因为函数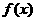 在区间
在区间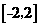 上不是单调函数,所以对称轴
上不是单调函数,所以对称轴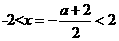 ,
,
解得: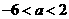 …………13分
…………13分
18.(1)∵A中有两个元素,∴关于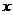 的方程
的方程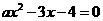 有两个不等的实数根,
有两个不等的实数根,
∴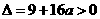 ,且
,且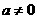 ,即所求的范围是
,即所求的范围是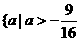 ,且
,且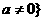 ;……6分
;……6分
(2)当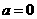 时,方程为
时,方程为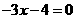 ,∴集合A=
,∴集合A=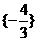 ;
;
当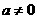 时,若关于
时,若关于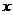 的方程
的方程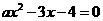 有两个相等的实数根,则A也只有一个元素,此时
有两个相等的实数根,则A也只有一个元素,此时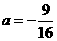 ;若关于
;若关于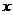 的方程
的方程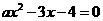 没有实数根,则A没有元素,此时
没有实数根,则A没有元素,此时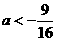 ,
,
综合知此时所求的范围是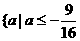 ,或
,或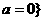 .………13分
.………13分
17.解:(1)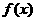 的定义域为
的定义域为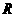 ,又
,又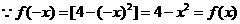 ,
,
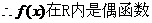 。……………3分
。……………3分
设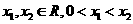 ,
,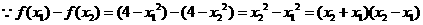
又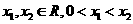 ,
,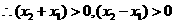
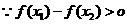
所以函数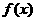 在
在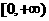 是减函数;……………7分
是减函数;……………7分
(2)依题意,得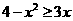 ,…………9分
,…………9分
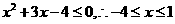 ,所以不等式
,所以不等式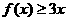 的解集为
的解集为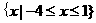 …………13分
…………13分
16.解:(1)A=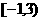 ,B=
,B=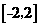
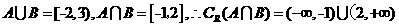 ………………6分
………………6分
(2)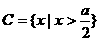 ,
,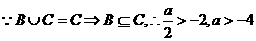 . ……………12分
. ……………12分
 实数
实数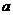 的取值范围是
的取值范围是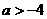 ……………13分
……………13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com