
题目列表(包括答案和解析)
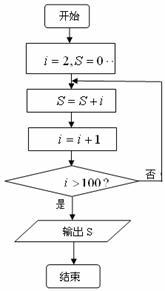
6.右图中,程序框图的循环体执行的次数是 ( )
A.100
B.99
C.98
D.97
5.在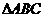 中,
中,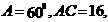 面积
面积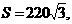 则
则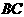 的长为 ( )
的长为 ( )
 A.75 B.51 C.49 D.
A.75 B.51 C.49 D.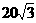
4.一枚硬币连掷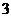 次,恰有两次正面朝上的概率是 ( )
次,恰有两次正面朝上的概率是 ( )
A.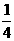 B.
B.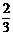 C.
C.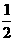 D.
D.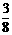
3.三鹿婴幼儿奶粉事件发生后,质检总局紧急开展了关于液态奶三聚氰胺的专项检查。假设蒙牛,伊利,光明三家公司生产的某批次液态奶分别是
 箱,
箱, 箱和
箱和 箱,现分层随机抽取
箱,现分层随机抽取 箱进行检验,则蒙牛、光明这两家公司生产的液态奶被抽取箱数之和为 ( )
箱进行检验,则蒙牛、光明这两家公司生产的液态奶被抽取箱数之和为 ( )
A.300 B.380 C.320 D.500
2.已知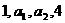 成等差数列,
成等差数列,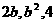 成等比数列,则
成等比数列,则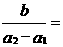 ( )
( )
A.2 B.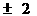 C.
C.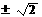 D.
D.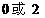
1.若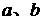 是任意实数,且
是任意实数,且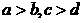 ,则 ( )
,则 ( )
A.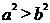 B.
B.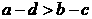 C.
C.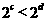 D.
D.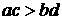
20、(本小题满分14分)
已知圆C过点P(1,1)且与圆M: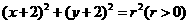 关于直线
关于直线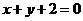 对称
对称
(1)求圆C的方程
(2)设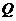 为圆C上一个动点,求
为圆C上一个动点,求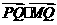 的最小值
的最小值
(3)过点P作两条相异直线分别与圆C相交于A、B两点,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP与AB是否平行,并请说明理由.
解:(1)依题意,可设圆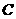 的方程为
的方程为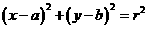 ,且
,且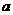 、
、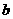 满足方程组
满足方程组
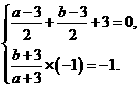 ………………2分
………………2分
由此解得 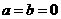 .又因为点
.又因为点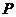
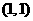 在圆
在圆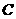 上,所以
上,所以
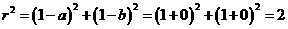 .故圆
.故圆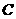 的方程为
的方程为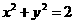 .…4分
.…4分
(2)设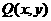 则
则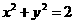 ,且
,且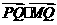 =
=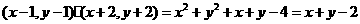 …………6分
…………6分
设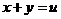 ,则由
,则由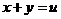 与圆
与圆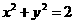 相交,求得
相交,求得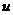 的取值范围为[-2,2]
的取值范围为[-2,2]
则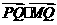 的最小值为了
的最小值为了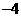 …………8分
…………8分
或者令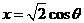 ,
,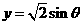 ,则
,则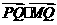 =
=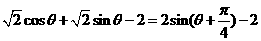
因为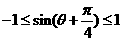 ,则
,则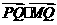 的最小值为了
的最小值为了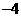 …………8分
…………8分
(3)由题意可知,直线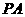 和直线
和直线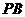 的斜率存在且互为相反数,
的斜率存在且互为相反数,
故可设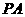 所在的直线方程为
所在的直线方程为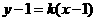 ,
, 所在的直线方程为
所在的直线方程为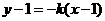 .…9分
.…9分
由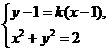 消去
消去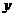 ,并整理得 :
,并整理得 :
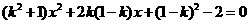 . ① …………10分
. ① …………10分
设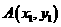 ,又已知P
,又已知P 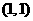 的横坐标1一定是该议程的根,则
的横坐标1一定是该议程的根,则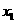 、1为方程①的两相异实数根,由根与系数的关系得
、1为方程①的两相异实数根,由根与系数的关系得 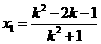 .同理,若设点B
.同理,若设点B 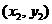 ,则可得
,则可得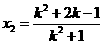 .…12分
.…12分
于是 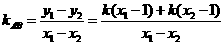 =
=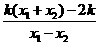 =1. ……13分
=1. ……13分
而直线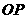 的斜率也是1,且两直线不重合,因此,直线
的斜率也是1,且两直线不重合,因此,直线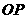 与
与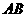 平行.…………14分
平行.…………14分
19、(本小题满分14分)
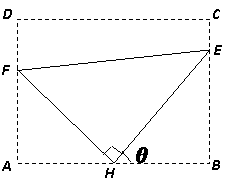
如图:某污水处理厂要在一个矩形污水处理池 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道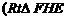 ,
,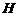 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口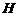 是
是 的中点,
的中点,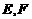 分别落在线段
分别落在线段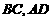 上.已知
上.已知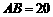 米,
米,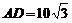 米,记
米,记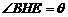 .
.
 (1)试将污水净化管道的长度
(1)试将污水净化管道的长度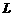 表示为
表示为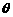 的函数,并写出定义域;
的函数,并写出定义域;
(2)若 ,求此时管道的长度
,求此时管道的长度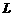 ;
;
(3)问:当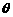 取何值时,污水净化效果最好?并求出此时
取何值时,污水净化效果最好?并求出此时
管道的长度.
答案1、解:(1)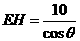 ,
,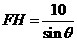 …………2分
…………2分
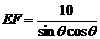 ……………………………………………………4分
……………………………………………………4分
由于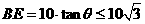 ,
,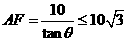
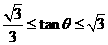 ,
, 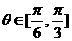 …………………………………………………5分
…………………………………………………5分
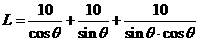 ,
, 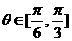 .……………………………6分
.……………………………6分
(2)  时,
时,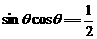 ,………………………………………7分
,………………………………………7分
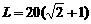 ;……………………………………………………………………8分
;……………………………………………………………………8分
(3)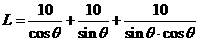 =
=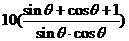
设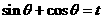 则
则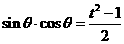 ……………………………………10分
……………………………………10分
由于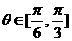 ,所以
,所以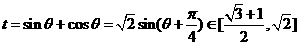 …12分
…12分
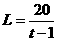 在
在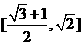 内单调递减,于是当
内单调递减,于是当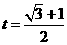 时
时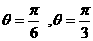 时
时
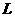 的最大值
的最大值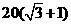 米. ………………………………………………………13分
米. ………………………………………………………13分
答:当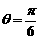 或
或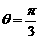 时所铺设的管道最短,为
时所铺设的管道最短,为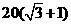 米.………………14分
米.………………14分
18、(本小题满分14分)
设平面内有四个向量 、
、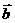 、
、 、
、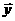 ,且满足
,且满足 =
=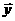 -
- ,
, 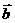 =2
=2 -
-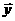 ,
, ⊥
⊥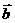 , |
, | |=|
|=|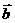 |=1.高&考%资*源#网
|=1.高&考%资*源#网
(1)求| |,|
|,|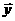 |;
|;
(2)若 、
、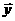 的夹角为
的夹角为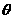 ,求cos
,求cos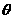 .
.
解:(1)
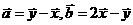
|
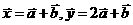
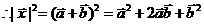
|
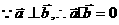
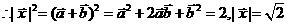
|
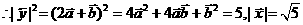
|
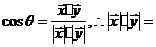
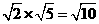
|
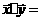
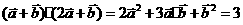
|

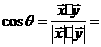
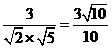
17、(本小题满分14分)
已知函数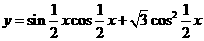 +1,求:
+1,求:
(1)求函数的单调减区间;
(2)求函数的最大值,以及函数取得最大值时自变量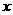 的集合
的集合
解:(1)将函数化简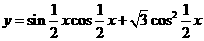 +1=
+1=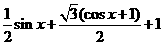
|
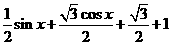 =
=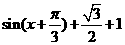
|
 当
当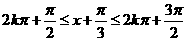 时,即
时,即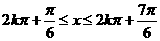
|
 函数的单调减区间为
函数的单调减区间为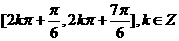 。
。
|
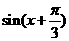 =1时,函数取得最大值为
=1时,函数取得最大值为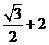 ,
,
此时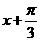 =
=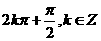
|
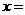
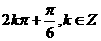 ,
,
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com