
题目列表(包括答案和解析)
9.一束光线从点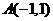 出发,经x轴反射到圆
出发,经x轴反射到圆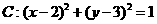 上的最短路径
上的最短路径
是
A.4
B.5 C.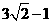 D.
D.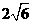
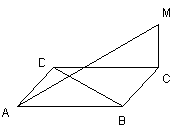
8.如图,如果 ⊥菱形
⊥菱形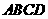 所在的平面,
所在的平面,
那么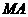 与
与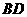 的位置关系是
的位置关系是
A.平行 B.垂直相交
C.异面 D.相交但不垂直
7.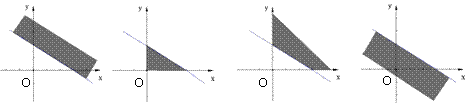 不等式
不等式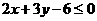 表示的平面区域是
表示的平面区域是
A. B. C. D.
6.直线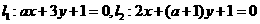 , 若
, 若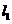 ∥
∥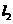 ,则
,则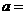
A.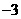 B.
B.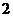 C.
C.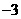 或
或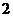 D.
D.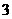 或
或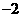
5.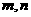 是两条不同直线,
是两条不同直线,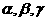 是三个不同平面,下列命题中正确的是
是三个不同平面,下列命题中正确的是
A.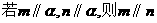 B.
B.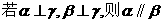
C.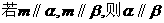 D.
D.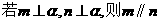
4.有下列四个命题:(1)过三点确定一个平面;(2)矩形是平面图形;(3)三条直线两
两相交则确定一个平面;(4)两个相交平面把空间分成四个区域其中错误命题的序号是
A.(1)和(2) B.(1)和(3)) C.(2)和(4) D.(2)和(3)
3.若一个几何体的主视图和侧视图都是等腰梯形,则这个几何体可能是
A.圆柱 B.棱锥 C.球体 D.圆台
2.已知△ABC的三个顶点为A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的中线长为
A.5 B.4 C.3 D.2
1.若直线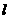 经过原点和点
经过原点和点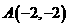 ,则它的斜率为
,则它的斜率为
A.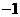 B.
B.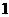 C.
C.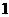 或
或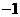 D.
D.
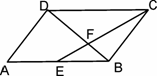 (17)(本题满分10分)
(17)(本题满分10分)
在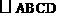 中,点E是AB的中点,点F在BD上,且BF=
中,点E是AB的中点,点F在BD上,且BF=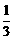 BD,求证:E、F、C三点共线.
BD,求证:E、F、C三点共线.
(18)(本题满分12分)
(Ⅰ)已知: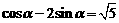 ,求
,求 的值.
的值.
(Ⅱ)已知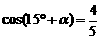 ,
,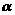 为锐角,求
为锐角,求 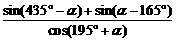 的值.
的值.
(19)(本题满分12分)
设向量a =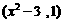 , b =
, b =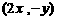 (其中实数
(其中实数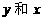 不同时为零),当
不同时为零),当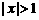 时,有a⊥b;当
时,有a⊥b;当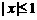 时,有a∥b.
时,有a∥b.
(Ⅰ)求函数解析式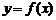 ;
;
(Ⅱ)设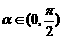 ,且
,且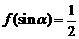 ,求
,求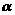 .
.
(20)(本题满分12分)
已知函数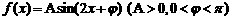 ,
,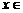 R的最大值是1,其图像经过
R的最大值是1,其图像经过
点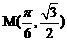 .
.
(Ⅰ)求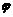 ;
;
(Ⅱ)求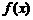 的单调递增区间;
的单调递增区间;
(Ⅲ)函数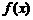 的图象经过怎样的平移可使其对应的函数成为奇函数
的图象经过怎样的平移可使其对应的函数成为奇函数
(21)(本题满分12分)
若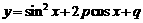 有最大值9和最小值3,求实数
有最大值9和最小值3,求实数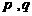 的值
的值
(22)(本题满分12分)
已知函数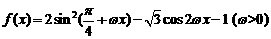 的最小正周期为
的最小正周期为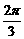
(Ⅰ)求 的值;
的值;
(Ⅱ)若不等式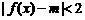 在
在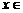
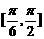 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
|

|
本溪市2010年7月普通高中模块结业验收考试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com