
题目列表(包括答案和解析)
12、在等比数列{an}中,a1a3=36,a2+a4=60,Sn>400,求n的范围。
解:∵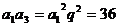 ,∴
,∴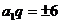
又∵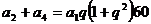 ,且
,且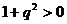 ,∴
,∴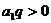 ,
,
∴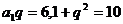 解之:
解之: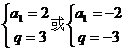
当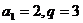 时,
时,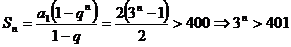 ,∴
,∴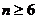
(∵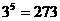
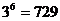 )
)
当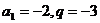 时,
时,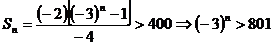 ,
,
∵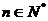 且必须为偶数
且必须为偶数
∴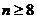 ,(∵
,(∵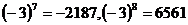 )
)
11、已知线段AB=a,P1为线段AB的中点,P2为BP1的中点,P3为P1P2的中点,P4为P2P3的中点,…, Pn为Pn-2Pn-1的中点,求APn的长.
解: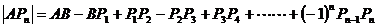
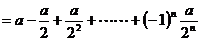
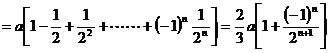
10、已知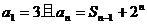 ,求
,求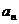 及
及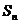 .
.
解:∵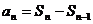 ∴
∴
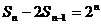 ∴
∴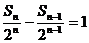
设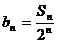 则
则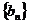 是公差为1的等差数列 ∴
是公差为1的等差数列 ∴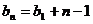
又:∵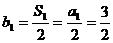 ∴
∴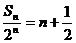 ∴
∴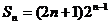
当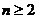 时
时 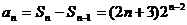
∴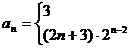
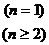
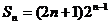
8、已知数列{an}的前n项和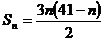 ,试求数列
,试求数列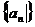 前30项的和. 9、已知
前30项的和. 9、已知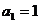 ,
,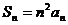
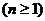 求
求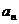 及
及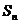 .
.
解: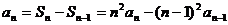 从而有
从而有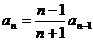
∵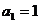 ∴
∴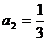
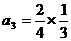
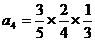
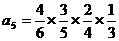
∴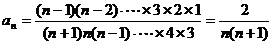 ∴
∴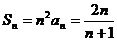
7、等差数列{an}中,a1>0, 前n项和为Sn,且S7=S13, 问n为何值时Sn最大?
解:(解法一)设公差为d,当d≥0时,则an=a1+(n-1)d>0.
∴Sn是关于n的单调递增数列,与S7=S13矛盾,故d<0.
又∵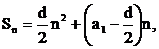 ∴点(n,Sn)在开口向下的抛物线上,
∴点(n,Sn)在开口向下的抛物线上,
∴当n=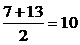 时, Sn最大.
时, Sn最大.
(解法二)由S7=S13知a8+a9+…+a12+a13=0,∵a8+a12=2a10, a9+a13=2a11,
∴a10+a11=0,设公差为d,当d≥0时,由a1>0,知a10>0,a11>0,与a10+a11=0矛盾.
故当d<0时, a10>a11,又a10+a11=0, ∴a10>0,a11<0,故Sn最大.
∴当n=10时,Sn最大.
6、已知等差数列的前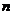 项和为
项和为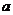 ,前
,前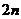 项和为
项和为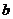 ,求前
,求前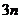 项和.
项和.
解:由题设 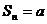
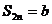
∴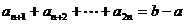 而
而
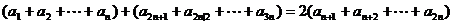
从而:
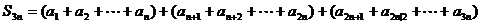
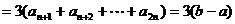
5、在等差数列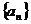 中,若
中,若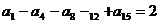 求
求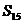 .
.
解:∵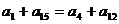 ∴
∴ 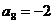 而
而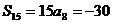
4、成等差数列的四个数之和为26,第二数和第三数之积为40,求这四个数.
解:设四个数为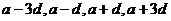
则: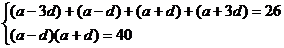
由①: 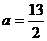 代入②得:
代入②得:
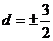
∴ 四个数为2,5,8,11或11,8,5,2.
3、实数a,b,5a,7,3b,…,c组成等差数列,且a+b+5a+7+3b+…+c=2500,求a,b,c的值.
解:由题设2b=a+5a,得b=3a;又14=5a+3b,∴a=1,b=3;
即a1=1,d=2.又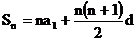 ,∴2500=
,∴2500=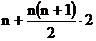 ,
,
∴n=50,a50=c=1+(50-1)2=99,∴a=1,b=3,c=99.
2、等差数列{an}中,a1>0,7a5=12a9,问n为何值时Sn最大.
解:由7(a1+4d)=12(a1+8d),∴d=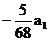 ,∴an=
,∴an=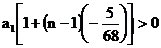
解得n<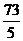 ,又n∈N*,∴当n=14时,S14最大.
,又n∈N*,∴当n=14时,S14最大.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com