6．方程2^－x+x²＝3的实数解的个数为________．

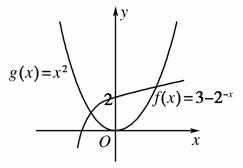
[解析]　分别作出函数f(x)=3-2-x与函数g(x)=x2的图象，如图所示．

∵f(0)=2，g(0)=0，∴从图象上可以看出它们有2个交点．

[答案]　2

5．已知对于任意实数x，函数f(x)满足f(－x)＝f(x)．若f(x)有2 009个零点，则这2 009个零点之和为________．

[解析]　设x₀为其中一根，即f(x₀)＝0，因为函数f(x)满足f(－x)＝f(x)，所以f(－x₀)＝f(x₀)＝0，

即－x₀也为方程一根，又因为方程f(x)＝0有2 009个实数解，所以其中必有一根x₁，满足x₁＝－x₁，即x₁＝0，所以这2 009个实数解之和为0.

[答案]　0

4．若函数f(x)的零点与g(x)＝4^x+2x－2的零点之差的绝对值不超过0.25，则f(x)可以是(　)

A．f(x)＝4x－1　 B．f(x)＝(x－1)²

C．f(x)＝e^x－1　 D．f(x)＝ln

[解析]　4个选项中的零点是确定的．

A：x＝；B：x＝1；C：x＝0；D：x＝.

又∵g(0)＝4⁰+2×0－2＝－1<0，

g＝4+2×－2＝1>0，

∴g(x)＝4^x+2x－2的零点介于之间．从而选A.

[答案]　A

3．设函数f(x)＝x³－^x－2的零点为x₀，则x₀所在的区间是(　)

A．(0,1)　 B．(1,2)

C．(2,3)　 D．(3,4)

[解析]　解法一：令f(x)＝x³－()^x－2，

则f(0)＝0－()^－2＝－4<0，

f(1)＝1－()^－2＝－1<0，

f(2)＝2³－()⁰＝7>0，

f(3)＝27－()¹＝26>0，

f(4)＝4³－()²＝63>0，

∴f(1)·f(2)<0，

故x₀所在的区间是(1,2)．

解法二：数形结合法，如图所示．

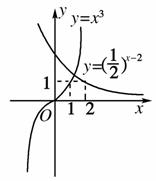
[答案]　B

2．函数f(x)＝ax²+2ax+c(a≠0)的一个零点是－3，则它的另一个零点是(　)

A．－1　 B．1

C．－2　 D．2

[解析]　由根与系数的关系得

－3+x＝－，∴x＝1.

即另一个零点是1，故选B.

[答案]　B

1．函数f(x)＝x²+x+3的零点的个数是(　)

A．0　 B．1

C．2　 D．3

[解析]　方程x²+x+3＝0中，判别式Δ＝－11<0，故方程无实根，函数没有零点．

[答案]　A

9．(10分)若x>0，y>0，且x－－2y＝0，求的值．

[解析]　∵x－－2y＝0，x>0，y>0，

∴()²－－2()²＝0，

∴(+)(－2)＝0，

由x>0，y>0得+>0，

∴－2＝0，∴x＝4y，

∴＝＝.

8．计算下列各式的值．

(1)；

(2)()³；

(3)；

(4).

[解析]　(1)根据x取值的不同，所得结果不同，注意分类讨论．

＝|x－2|＝

(2)()³＝－2；

(3)＝＝π－3；

(4)＝＝2.

7．求－+的值．

[解析]　原式＝－+

＝－+＝.

6．下列各式总能成立的是________．

(1)(－)⁴＝a－b

(2)()⁴＝a+b

(3)＝a－b

(4)＝a+b

[解析]　要注意()ⁿ与的区别，当n为大于1的奇数时，()ⁿ＝；当n为大于1的偶数时，()ⁿ＝a，＝|a|，这是因为意味着a≥0，而中a可以为任意实数．因此，(3)、(4)不恒成立．选项(1)中，当a＝b≥0时才能成立．故(2)成立．

[答案]　(2)