
题目列表(包括答案和解析)
例1. 解同余式。
1)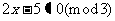
2)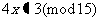
3)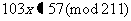
4)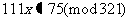
例2. 解同余方程组。
1)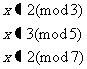 2)
2)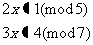 3)
3)
例3. 求出最小的正整数,它的一半是整数的平方,它的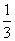 是整数的三次方,它的
是整数的三次方,它的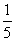 是整数的五次方。
是整数的五次方。
例4. 解二元一次不定方程。
1)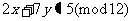
2)求: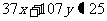 的整数解
的整数解
高斯函数
2.定理: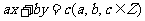 有解
有解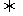
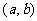 ︱c
︱c
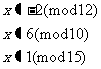
1.形式: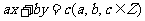
2.讨论
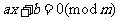 的解
的解
分析:1)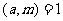
设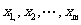 是模m的完系,因为
是模m的完系,因为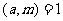 ,所以
,所以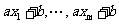 也是模m的完系。因此,其中必有且只有一个树与零同余,即
也是模m的完系。因此,其中必有且只有一个树与零同余,即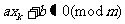 ,即(1)有唯一解。
,即(1)有唯一解。
由(1)得: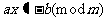 ,由欧拉定理知:
,由欧拉定理知: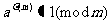 ,所以
,所以
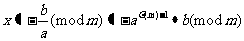
2)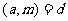 >1
>1
设(1)有解,则d︱b;反过来,设d︱b,因为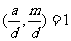 ,所以
,所以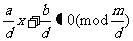 ……(2)有解,所以(1)有解。所以,(1)和(2)是等价的。下面求(2)的解即可。但是要注意,(1)和(2)的模不同,所以(2)的相同的解不一定也是(1)的相同的解,下面我们在(2)的所有解中来求(1)的所有不相同的解。
……(2)有解,所以(1)有解。所以,(1)和(2)是等价的。下面求(2)的解即可。但是要注意,(1)和(2)的模不同,所以(2)的相同的解不一定也是(1)的相同的解,下面我们在(2)的所有解中来求(1)的所有不相同的解。
设(2) 的唯一解为: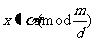 ,则所以形如
,则所以形如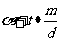 (t为任意整数)的数都是(2)的解,因此这些数中所有关于模m不同余的数就是(1)的所有解。
(t为任意整数)的数都是(2)的解,因此这些数中所有关于模m不同余的数就是(1)的所有解。
因为当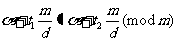 ……(3)时,有
……(3)时,有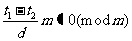 ,所以
,所以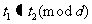 ;反之也成立,所以(3)成立的充要条件是
;反之也成立,所以(3)成立的充要条件是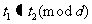
因此,在所有形如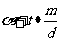 的数中只要t取关于模d不同余的数,所得到的数就关于模m不同余,所以
的数中只要t取关于模d不同余的数,所得到的数就关于模m不同余,所以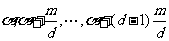 就是(1)的所有解。
就是(1)的所有解。
定理1 一元一次同余方程中,
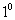 当
当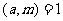 ,有唯一解,
,有唯一解,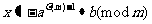
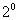
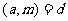 >1,
>1,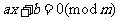 有解
有解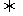 d︱b,
d︱b,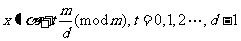 , 其中
, 其中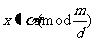 是
是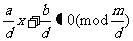 的唯一解。
的唯一解。
定理2
(中国剩余定理)设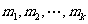 两两互质,
两两互质,
则同余方程组
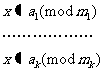 (4)
(4)
对于模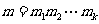 有唯一解:
有唯一解: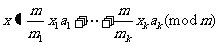
其中: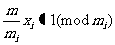 ,
,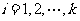
1.形式: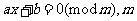 不能整除
不能整除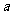 ………………(1)
………………(1)
例1.数列{an}的二阶差数列的各项均为16,且a63=a89=10,求a51
解:法一:显然{an}的二阶差数列{bn}是公差为16的等差数列,设其首项为a,则bn=a+(n-1)×16,于是an= a1+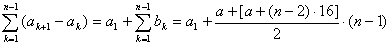
=a1+(n-1)a+8(n-1)(n-2)
这是一个关于n的二次多项式,其中n2的系数为8,由于a63=a89=10,所以
an=8(n-63)(n-89)+10,从而a51=8(51-63)(51-89)+10=3658
解:法二:由题意,数列{an}是二阶等差数列,故其通项是n的二次多项式,又a63=a89=10,故可设an=A(n-63)(n-89)+10
由于{an}是二阶差数列的各项均为16,所以(a3-a2)-(a2-a1)=16
即a3-2a2+a1=16,所以
A(3-63)(3-89)+10-2[A(2-63)(2-89)+10]+A(1-63)×(1-89)+10=16
解得:A=8
an=8(n-63)(n-89)+10,从而a51=8(51-63)(51-89)+10=3658
例2.一个三阶等差数列{an}的前4项依次为30,72,140,240,求其通项公式
解:由性质(2),an是n的三次多项式,可设an=An3+Bn2+Cn+D
由a1=30、a2=72、a3=140、a4=240得
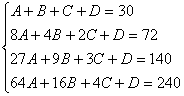 解得:
解得: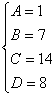
所以an=n3+7n2+14n+8
例3.求和:Sn=1×3×22+2×4×32+…+n(n+2)(n+1)2
解:Sn是是数列{n(n+2)(n+1)2}的前n项和,
因为an=n(n+2)(n+1)2是关于n的四次多项式,所以{an}是四阶等差数列,于是Sn是关于n的五次多项式
k(k+2)(k+1)2=k(k+1)(k+2)(k+3)-2k(k+1)(k+2),故求Sn可转化为求
Kn=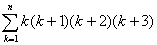 和Tn=
和Tn=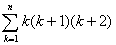
k(k+1)(k+2)(k+3)=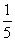 [
k(k+1)(k+2)(k+3)(k+4)-(k-1) k(k+1)(k+2)(k+3)],所以
[
k(k+1)(k+2)(k+3)(k+4)-(k-1) k(k+1)(k+2)(k+3)],所以
Kn=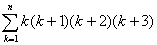 =
=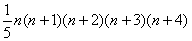
Tn=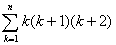 =
=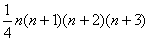
从而Sn=Kn-2Tn=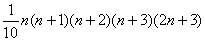
例4.已知整数列{an}适合条件:
(1)an+2=3an+1-3an+an-1,n=2,3,4,…
(2)2a2=a1+a3-2
(3)a5-a4=9,a1=1
求数列{an}的前n项和Sn
解:设bn=an+1-an,Cn=bn+1-bn
Cn=bn+1-bn= (an+2-an+1)-( an+1-an)=an+2-2an+1+an=(3an+1-3an+an-1) -2an+1+an=an+1-2an+an-1
=Cn-1 (n=2,3,4,…)
所以{ Cn}是常数列
由条件(2)得C1=2,则{an}是二阶等差数列
因此an=a1+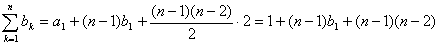
由条件(3)知b4=9,从而b1=3,于是an=n2
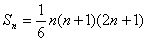
例5.求证:二阶等差数列的通项公式为
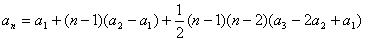
证明:设{an}的一阶差数列为{bn},二阶差数列为{cn},由于{an}是二阶等差数列,故{cn}为常数列
又c1=b2-b1=a3-2a2+a1
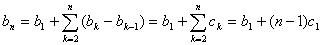 所以
所以
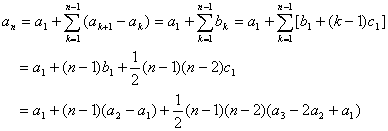
例6.求数列1,3+5+7,9+11+13+15+17,…的通项
解:问题等价于:将正奇数1,3,5,…按照“第n个组含有2n-1个数”的规则分组:
(1)、(3,5,7)、(9,11,13,15,17),… 然后求第n组中各数之和an
依分组规则,第n组中的数恰好构成以2为公差的项数为2n-1的等差数列,因而确定了第n组中正中央这一项,然后乘以(2n-1)即得an
将每一组的正中央一项依次写出得数列:1,5,13,25,…这个数列恰为一个二阶等差数列,不难求其通项为2n2-2n+1,故第n组正中央的那一项为2n2-2n+1,从而
an=(2n-2n+1)(2n-1)
例7.数列{an}的二阶差数列是等比数列,且a1=5,a2=6,a3=9,a4=16,求{an}的通项公式
解:易算出{an}的二阶差数列{cn}是以2为首项,2为公比的等比数列,则cn=2n,
{an}的一阶差数列设为{bn},则b1=1且
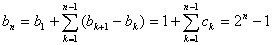
从而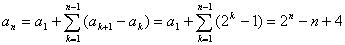
例8.设有边长为1米的正方形纸一张,若将这张纸剪成一边长为别为1厘米、3厘米、…、(2n-1)厘米的正方形,愉好是n个而不剩余纸,这可能吗?
解:原问题即是是否存在正整数n,使得12+32+…+(2n-1)2=1002
由于12+32+…+(2n-1)2=[12+22+…+(2n)2]-[22+42+…+(2n)2]=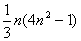 随着n的增大而增大,当n=19时
随着n的增大而增大,当n=19时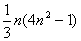 =9129<10000,当n=20时
=9129<10000,当n=20时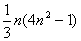 =10660>10000
=10660>10000
故不存在…
例9.对于任一实数序列A={a1,a2,a3,…},定义DA为序列{a2-a1,a3-a2,…},它的第n项为an+1-an,假设序列D(DA)的所有项均为1,且a19=a92=0,求a1
解:设序列DA的首项为d,则序列DA为{d,d+1,d+2,…},它的第n项是d+(n-1),因此序列A的第n项
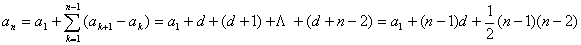 显然an是关于n的二次多项式,首项等比数列为
显然an是关于n的二次多项式,首项等比数列为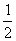
由于a19=a92=0,必有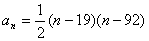
所以a1=819
5.高阶等差数列中最重要也最常见的问题是求通项和前n项和,更深层次的问题是差分方程的求解,解决问题的基本方法有:
(1)逐差法:其出发点是an=a1+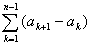
(2)待定系数法:在已知阶数的等差数列中,其通项an与前n项和Sn是确定次数的多项式(关于n的),先设出多项式的系数,再代入已知条件解方程组即得
(3)裂项相消法:其出发点是an能写成an=f(n+1)-f(n)
(4)化归法:把高阶等差数列的问题转化为易求的同阶等差数列或低阶等差数列的问题,达到简化的目的
4.高阶等差数列的性质:
(1)如果数列{an}是p阶等差数列,则它的一阶差数列是p-1阶等差数列
(2)数列{an}是p阶等差数列的充要条件是:数列{an}的通项是关于n的p次多项式
(3) 如果数列{an}是p阶等差数列,则其前n项和Sn是关于n的p+1次多项式
3.高阶等差数列是二阶或二阶以上等差数列的统称
2.如果某数列的p阶差数列是一非零常数列,则称此数列为p阶等差数列
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com