16．有下列四个命题：

①函数f(x)＝为偶函数；

②函数y＝的值域为{y|y≥0}；

③已知集合A＝{－1,3}，B＝{x|ax－1＝0，a∈R}，若A∪B＝A，则a的取值集合为{－1，}；

④集合A＝{非负实数}，B＝{实数}，对应法则f：“求平方根”，则f是A到B的映射．你认为正确命题的序号为：________.

[解析]　函数f(x)＝的定义域为(－∞，2)∪

(2，+∞)，它关于坐标原点不对称，所以函数f(x)＝既不是奇函数也不是偶函数，即命题①不正确；

函数y＝的定义域为{x|x≥1}，当x≥1时，y≥0，即命题②正确；

因为A∪B＝A，所以B⊆A，若B＝Ø，满足B⊆A，这时a＝0；若B≠Ø，由B⊆A，得a＝－1或a＝.因此，满足题设的实数a的取值集合为{－1,0，}，即命题③不正确；依据映射的定义知，命题④正确．

[答案]　②④

15．函数f(x)＝x²－2x的单调递减区间是________．

[解析]　该函数是复合函数，可利用判断复合函数单调性的方法来求解，因为函数y＝^u是关于u的减函数，所以内函数u＝x²－2x的递增区间就是函数f(x)的递减区间．令u＝x²－2x，其递增区间为[1，+∞)，根据函数y＝^u是定义域上的减函数知，函数f(x)的减区间就是[1，+∞)．

[答案]　[1，+∞)

14．已知集合A＝{x|log₂x≤2}，B＝(－∞，a)，若A⊆B，则实数a的取值范围是(c，+∞)，其中c＝________.

[解析]　A＝{x|0<x≤4}，B＝(－∞，a)．若A⊆B，则a>4，即a的取值范围为(4，+∞)，∴c＝4.

[答案]　4

13．已知全集U＝{2,3，a²－a－1}，A＝{2,3}，若∁_UA＝{1}，则实数a的值是________．

[答案]　－1或2

12．已知f(x)是偶函数，它在[0，+∞)上是减函数．若f(lg x)>f(1)，则x的取值范围是(　)

A.　 B.∪(1，+∞)

C.　 D．(0,1)∪(10，+∞)

[解析]　由已知偶函数f(x)在[0，+∞)上递减，

则f(x)在(－∞，0)上递增，

∴f(lg x)>f(1)⇔0≤lg x<1，或

⇔1≤x<10，或⇔1≤x<10，

或<x<1⇔<x<10，

∴x的取值范围是.故选C.

[答案]　C

11．设log₃2＝a，则log₃8－2 log₃6可表示为(　)

A．a－2　 B．3a－(1+a)²

C．5a－2　 D．1+3a－a²

[解析]　log₃8－2log₃6＝log₃2³－2log₃(2×3)

＝3log₃2－2(log₃2+log₃3)

＝3a－2(a+1)＝a－2.故选A.

[答案]　A

10．某新品牌电视投放市场后第1个月销售100台，第2个月销售200台，第3个月销售400台，第4个月销售790台，则下列函数模型中能较好反映销量y与投放市场的月数x之间的关系的是(　)

A．y＝100x　 B．y＝50x²－50x+100

C．y＝50×2^x　 D．y＝100log₂x+100

[解析]　对C，当x＝1时，y＝100；

当x＝2时，y＝200；

当x＝3时，y＝400；

当x＝4时，y＝800，与第4个月销售790台比较接近．故选C.

[答案]　C

9．函数f(x)＝x²+(3a+1)x+2a在(－∞，4)上为减函数，则实数a的取值范围是(　)

A．a≤－3　 B．a≤3

C．a≤5　 D．a＝－3

[解析]　函数f(x)的对称轴为x＝－，

要使函数在(－∞，4)上为减函数，

只须使(－∞，4)⊆(－∞，－)

即－≥4，∴a≤－3，故选A.

[答案]　A

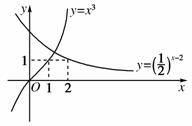
8．设函数y＝x³与y＝^x－2的图象的交点为(x₀，y₀)，则x₀所在的区间是(　)

A．(0,1)　 B．(1,2)

C(2,3)　 D．(3,4)

[解析]　由函数图象知，故选B.

[答案]　B

7．定义在R上的偶函数f(x)的部分图象如图所示，则在(－2,0)上，下列函数中与f(x)的单调性不同的是(　)

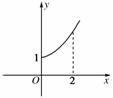
A．y=x2+1　 B．y＝|x|+1

C．y＝　 D．y＝

[解析]　∵f(x)为偶函数，由图象知f(x)在(－2,0)上为减函数，而y＝x³+1在(－∞，0)上为增函数．故选C.

[答案]　C