16.已知二次函数f(x)=(lga)x²+2x+4lga的最大值为3,求a的值.

解：原函数式可化成f(x)=lga(x+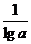)²-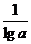+4lga.

由已知,f(x)有最大值3,

∴lga<0,并且-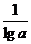+4lga=3,

整理得4(lga)²-3lga-1=0,

解得lga=1,lga=-.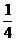

∵lga<0,故取lga=-.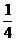

∴a=.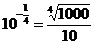

15.如果log₂［log₃(log₄x)］=log₃［log₄(log₂y)］=log₄［log₂(log₃z)］=0,则x+y-z等于(　　 )

A.70　　　　　　　　　 B.71　　　　　　　　　 C.89　　　　　　　 D.90

答案：B

解析：log₂［log₃(log₄x)］=0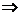log₃(log₄x)=1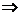log₄x=3.

∴x=4³=64.

同理,y=16,z=9.

∴x+y-z=71.

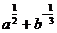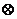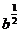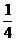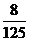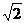
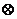
14.定义运算法则如下:a*b=,ab=lga²-lg,M=2*,N=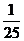,则M+N=_________________.

答案：5

解析：M=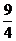*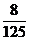==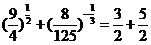4.

N=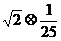

=lg2-lg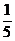=lg10=1.

∴M+N=5.

13.计算:

(1)log₂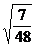+log₂12-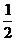log₂42;

(2)lg2·lg50-lg5·lg20-lg4.

解：(1)log₂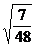+log₂12-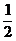log₂42

=log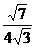₂［·12·］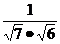

=log₂()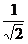

=log₂=-.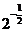

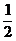(2)lg2·lg50-lg5·lg20-lg4=lg2(1+lg5)-lg5(1+lg2)-2lg2

=lg2-lg5-2lg2

=-(lg2+lg5)=-1.

拓展应用　 跳一跳，够得着！

12.已知a^m=2,aⁿ=3,求a^3m-2n的值.

解：∵a^m=2,aⁿ=3,

∴log_a2=m,log_a3=n.

∴a^3m-2n=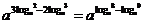

=.

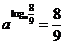11.已知a、b、c为△ABC的三边,且关于x的方程x²-2x+lg(c²-b²)-2lga+1=0有等根,判断△ABC的形状.

解：由题意可得Δ=0,

即4-4［lg(c²-b²)-2lga+1］=0.

∴2lga=lg(c²-b²),lga²=lg(c²-b²).

∴a²=c²-b²,

即a²+b²=c².

根据勾股定理可得△ABC是直角三角形.

10.已知f(x)=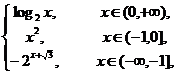 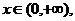则f{f［f(-2-3)］}=______________.

答案：-4

解析：∵-2-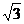<-1,

又∵x∈(-∞,-1)时,f(x)=-,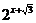

∴f(-2-)=- =-.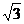

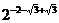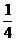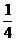∵-∈(-1,0］,

而x∈(-1,0)时,f(x)=x²,

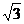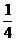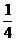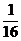∴f［f(-2-)］=f(-)=(-)²=>0.

而x∈(0,+∞)时,f(x)=log₂x,

∴f{f［f(-2-3)］}=f(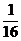)=log₂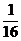=-4.

9.若lgx=a,lgy=b,则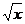lg-lg(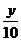)²的值为(　　 )

A.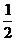a-2b-2　　　　　　　　　　　　 B.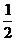a-2b+2

C.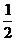a-2b-1　　　　　　　　　　　　 D.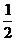a-2b+1

答案：B

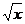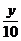解析：∵lg-lg()²=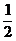lgx-2lg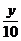

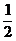=lgx-2(lgy-lg10)

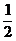=a-2(b-1)

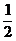=a-2b+2.

8.设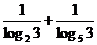=n,那么n的值属于下列哪一个区间?(　　 )

A.(2,3)　　　　　　　 B.(1,2)　　　　　　　 C.(-2,-1)　　　　　　　　 D.(-3,-2)

答案：A

解析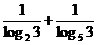：=log₃2+log₃5=log₃10,

2=log₃9<log₃10<log₃27=3.

∴2<n<3.

7.已知log₃2=a,3^b=5,试用a、b表示log₃.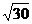

解：根据题意,得b=log₃5,

∴log₃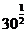=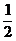log₃(3×10)=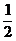(log₃3+log₃10)

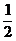=［1+log₃(2×5)］

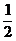=(1+log₃2+log₃5)

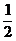=(1+a+b).

能力提升　 踮起脚,抓得住!