
题目列表(包括答案和解析)
9.式子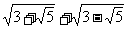 的化简结果为( )
的化简结果为( )
A.1
B.10
C.100
D.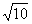
答案:D
解析:(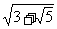 +
+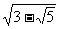 )2=3+
)2=3+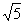 +2
+2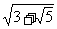
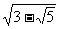 +3-
+3-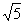
=6+2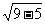 =10.
=10.
∴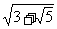 +
+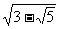 =
=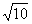 .
.
8.化简(-3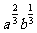 )(
)(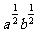 )÷(
)÷(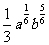 )得( )
)得( )
A.6a B.-a C.-9a D.9a
答案:C
解析:原式=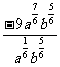 =-9a.
=-9a.
7.计算下列各式:
(1)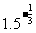 ×(-
×(-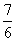 )0+80.25×
)0+80.25×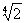 +(
+(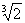 ×
×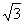 )6-
)6-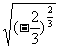 ;
;
(2)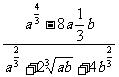 ÷(1-2
÷(1-2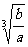 )×
)×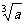 .
.
解:(1)原式=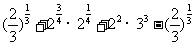 =21+4×27=110.
=21+4×27=110.
(2)原式=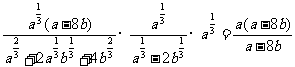 =a.
=a.
能力提升 踮起脚,抓得住!
6.已知2x-2-x=3,则4x+4-x=__________________.
答案:11
解析:(2x-2-x)2=9,即4x+4-x-2=9,则4x+4-x=11.
5.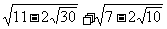 =___________________.
=___________________.
答案: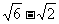
解析:原式=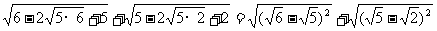
=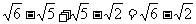 .
.
4.计算7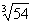 +3
+3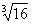 -7
-7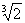 -5
-5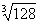 的结果是( )
的结果是( )
A.0
B.54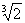 C.-6
C.-6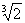 D.40
D.40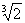
答案:A
解析:原式=7×3×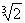 +3×2×
+3×2×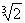 -7×
-7×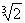 -5×4×
-5×4×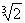 =27
=27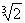 -27
-27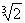 =0.
=0.
3.化简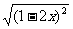 (x>
(x>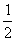 )的结果是( )
)的结果是( )
A.1-2x B.0
C.2x-1 D.(1-2x)2
答案:C
解析: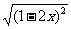 =|2x-1|,而x>
=|2x-1|,而x>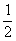 ,
,
∴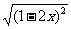 =2x-1.
=2x-1.
2.有下列四个命题:
(1)正数的偶次方根是一个正数;(2)正数的奇次方根是一个正数;(3)负数的偶次方根是一个负数;(4)负数的奇次方根是一个负数.
其中正确的个数是( )
A.0 B.1 C.2 D.3
答案:C
解析:其中(1)(3)错误,(2)(4)正确.
1.用分数指数幂表示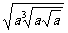 为( )
为( )
A.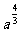 B.
B.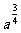 C.
C.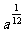 D.
D.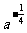
答案:B
解析:因为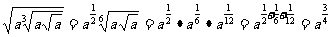 .
.
16.已知函数f(x)=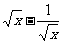 .
.
(1)证明函数f(x)在定义域上有反函数,并求出反函数;
(2)反函数的图象与直线y=x有无交点?
(1)证明:∵f(x)的定义域为正实数集,
∴当0<x1<x2时,f(x1)-f(x2)=(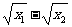 )-(
)-(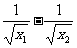 )=(
)=(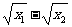 )(1+
)(1+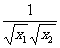 )<0.
)<0.
∴f(x1)<f(x2),即f(x)在(0,+∞)上是增函数.
∴f(x)有反函数.当x∈(0,+∞)时,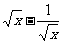 ∈(-∞,+∞).∴反函数的定义域为R.
∈(-∞,+∞).∴反函数的定义域为R.
由y=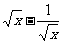 ,得x-y
,得x-y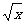 -1=0.
-1=0.
解得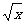 =
=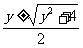 .∵y<
.∵y<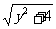 ,
,
∴y- <0.而
<0.而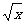 >0,
>0,
∴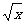 =
=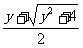 ,x=
,x=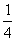 (y+
(y+ )2.
)2.
∴f-1(x)=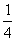 (x+
(x+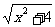 )2(x∈R).
)2(x∈R).
(2)解:y=f-1(x)与y=f(x)的图象关于y=x对称,故只需判断y=f(x)与y=x有无交点.
由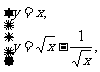 得x=
得x=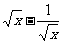 .
.
∴x(1-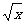 )=1.
)=1.
当0<x<1时,0<1-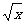 <1.∴0<x(1-
<1.∴0<x(1-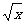 )<1,此时方程无实数根.
)<1,此时方程无实数根.
当x≥1时,x(1-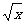 )≤0,方程无实根.
)≤0,方程无实根.
∴y=f(x)与y=x无交点.
从而y=f-1(x)与y=x无交点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com