
题目列表(包括答案和解析)
5、方程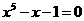 的一个正零点的存在区间可能是( )
的一个正零点的存在区间可能是( )
A、[0,1] B、[1,2] C、[2,3] D、[3,4]
4.若函数f(x)唯一的一个零点在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是( )
A、函数f(x)在区间(0,1)内有零点
B、函数f(x)在区间(0,1)或(1,2)内有零点
C、函数f(x)在区间(2,16)内有零点
D、函数f(x)在区间(1,16)内无零点
3.三次方程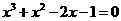 在下列那些连续整数之间有根( )
在下列那些连续整数之间有根( )
1)-2与-1之间 2)-1与0之间 3)0与1之间
4)1与2之间 5)2与3之间
A、1)2)3) B、1)2)4) C、1)2)5) D、2)3)4)
2.函数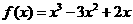 的零点个数为( )
的零点个数为( )
A、0 B、1 C、2 D、3
1.函数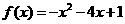 的零点为( )
的零点为( )
A、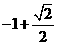 B、
B、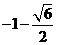 C、
C、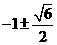 D、不存在
D、不存在
16.为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD(如图所示)上规划出一块长方形地面建住宅小区公园(公园的一边落在CD上),但不超过文物保护区△AEF的红线EF,问如何设计才能使公园占地面积最大?并求出最大面积.(已知AB=CD=200 m,BC=AD=160 m,AE=60 m,AF=40 m)
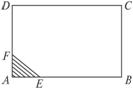
解:如图,作矩形MONC,其中O在EF上,过点F作FG⊥MO于G.
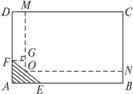
设MC=x(m),面积为y,则FG=DM=200-x(m),显然△OFG∽△FEA.
∴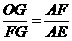 .
.
∴OG=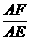 ·FG=
·FG=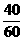 ×(200-x)
×(200-x)
=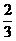 (200-x)(m).
(200-x)(m).
MG=DF=AD-AF=160-40=120(m).
∴OM=MG+OG=120+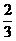 (200-x)=-
(200-x)=-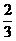 x+
x+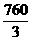 .
.
∴y=x(-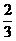 x+
x+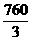 )=-
)=-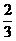 (x-190)2+
(x-190)2+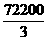 (0<x<200).
(0<x<200).
∴当且仅当x=190时,y有最大值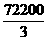 .
.
∴长方形公园在CD边上的边长为190 m时,面积最大,且最大面积为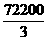 m2
m2
15.某厂原来月产量为a,一月份增产10%,二月份比一月份减产10%,设二月份产量为b,则( )
A.a=b B.a>b
C.a<b D.无法比较a、b的大小
答案:B
解析:∵b=a(1+10%)(1-10%),
∴b=a[1-(10%)2]=a(1-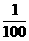 ).
).
∴b=a×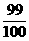 .
.
∴a>b.
14.某商场对顾客实行购物优惠活动,规定一次购物 (1)如不超过200元,则不予以优惠;(2)如果超过200元但不超过500元的按标价给予9折优惠; (3)如果超过500元,其中500元按第(2)条给予优惠,超过500元的部分,给予8折优惠.某人两次去购物,分别付款168元和423元.若他只去一次,购买同样的商品,则应付款是( )
A.472.8元 B.510.4元 C.522.8元 D.560.4元
答案:D
解析:168<200×90%,
∴第一次没有优惠.
423<500×90%,
∴第二次按九折优惠.
实际总价钱为168+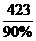 =638.
=638.
应付价钱为500×90%+138×80%=560.4.
13.某种商品进货价每件50元,据市场调查,当销售价格(每件x元)在50≤x≤80时,每天售出的件数P=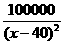 ,若想每天获得的利润最多,销售价每件应定为多少元?
,若想每天获得的利润最多,销售价每件应定为多少元?
解:设销售价定为每件x元,每天获利y元,
则y=(x-50)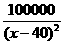 =100 000[
=100 000[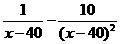 ].
].
令u=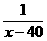 ,
,
则y=100 000(-10u2+u),
∴当u=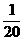 ,即x=60时,y取最大值.
,即x=60时,y取最大值.
∴销售价为每件60元时,获利最大.
拓展应用 跳一跳,够得着!
12.某公司拟投资100万元,有两种获利的可能可供选择:一种是年利率10%,按单利计算,5年后收回本金和利息;另一种是年利率9%,按每年复利一次计算,5年后收回本金和利息,哪一种投资更有利?5年后,这种投资比另一种投资可多得利息多少元?
解:本金100万元,年利率10%,按单利计算,5年后的本利和是100×(1+10%×5)=150(万元).
本金100万元,年利率9%,按每年复利一次计算,5年后的本利和是100×(1+9%)5=153.86(万元).
由此可见,按年利率9%每年复利一次计算的投资要比年利率10%单利计算的更有利,5年后多得利息3.86万元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com