
题目列表(包括答案和解析)
6.已知下面四个等式:(1)lg(ab)=lga+lgb;(2)lg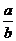 =lga-lgb;(3)
=lga-lgb;(3)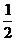 lg(
lg(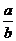 )2=lg
)2=lg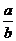 ;(4)lg(ab)=
;(4)lg(ab)=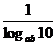 .
.
其中正确的命题的个数为_________________.
答案:0
解析:(1)(2)(3)(4)都是错误的,例如:
(1)lg[(-2)×(-3)]≠lg(-2)+lg(-3);
(2)lg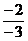 ≠lg(-2)-lg(-3);
≠lg(-2)-lg(-3);
(3)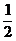 lg(
lg(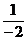 )2≠lg(
)2≠lg(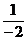 );
);
(4)lg(2×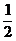 )≠
)≠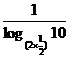 .
.
注意:在应用对数的性质时,一定要使运算过程中的每一个数式都有意义.
5.满足等式2lg(3x-2)=lgx+lg(3x+2)的实数x的值为______________.
答案:2
解析: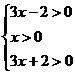
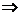 x>
x>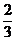 ,(3x-2)2=x(3x+2).
,(3x-2)2=x(3x+2).
解得x=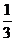 (舍)或x=2.
(舍)或x=2.
4.(四川成都模拟)lg8+3lg5的值为( )
A.-3 B.-1
C.1 D.3
答案:D
解析:原式=3lg2+3lg5=3lg10=3.
3.给出下列四个命题:①对数的真数是非负数;②若a>0且a≠1,则loga1=0;③若a>0且a≠1, logaa=1;④若a>0,且a≠1,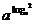 =2.其中正确的命题是( )
=2.其中正确的命题是( )
A.①②③ B.②③④
C.①③ D.①②③④
答案:B
解析:①对数的真数是正数而不是非负数,其他几个是正确的.
2.已知log7[log3(log2x)]=0,那么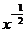 等于( )
等于( )
A.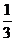 B.
B.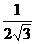
C.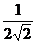 D.
D.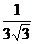
答案:C
解析:由外到里依次有log3(log2x)=1,log2x=3,x=23,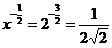 .
.
1.在y=log(x-2)(5-x)中,实数x的取值范围是( )
A.x>5或x<2 B.2<x<5
C.2<x<3或3<x<5 D.3<x<4
答案:C
解析: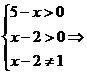 2<x<3或3<x<5.
2<x<3或3<x<5.
16.已知函数f(x)=ax+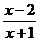 (a>1).
(a>1).
(1)证明函数f(x)在(-1,+∞)上为增函数;
(2)用反证法证明方程f(x)=0没有负数根.
证明:(1)任取x1、x2∈(-1,+∞),不妨设x1<x2,
则x1-x2<0,0<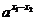 <1且
<1且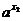 >0.
>0.
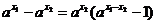 <0.
<0.
又x1+1>0,x2+1>0,
∴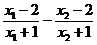
=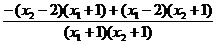
=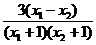 <0.
<0.
∴f(x1)-f(x2)=(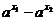 )+(
)+(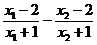 )<0,
)<0,
即f(x1)<f(x2).
∴f(x)在(-1,+∞)上是单调增函数.
(2)假设存在x0<0(x0≠-1)满足f(x0)=0,
则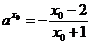 .
.
又0<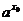 <1,
<1,
∴0<-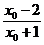 <1,
<1,
即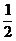 <x0<2与x0<0矛盾. ∴f(x)=0没有负数根.
<x0<2与x0<0矛盾. ∴f(x)=0没有负数根.
15.已知f(x)=3x-b(2≤x≤4,b为常数)的图象经过点(2,1),则F(x)=f2(x)-2f(x)的值域为( )
A.[-1,+∞) B.[-1,63)
C.[0,+∞) D.(0,63]
答案:B
解析:由f(2)=1,得32-b=1,b=2,f(x)=3x-2.
∴F(x)=[f(x)-1]2-1=(3x-2-1)2-1.
令t=3x-2,2≤x≤4.
∴g(t)=(t-1)2-1,t∈[1,9].
∴所求值域为[-1,63].
14.函数y=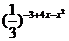 的单调递增区间是( )
的单调递增区间是( )
A.[1,2] B.[2,3] C.(-∞,2] D.[2,+∞)
答案:D
解析:因为y=3x2-4x+3,又y=3t单调递增,t=x2-4x+3在x∈[2,+∞)上递增,故所求的递增区间为[2,+∞).
13.已知关于x的方程2a2x-2-7ax-1+3=0有一个根是2,求a的值和方程其余的根.
解:∵2是方程2a2x-2-9ax-1+4=0的根,将x=2代入方程解得a=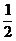 或a=4.
或a=4.
(1)当a=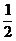 时,原方程化为2·(
时,原方程化为2·(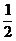 )2x-2-9(
)2x-2-9(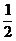 )x-1+4=0.
①
)x-1+4=0.
①
令y=(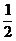 )x-1,方程①变为2y2-9y+4=0,
)x-1,方程①变为2y2-9y+4=0,
解得y1=4,y2=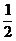 .
.
∴(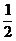 )x-1=4
)x-1=4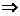 x=-1,
x=-1,
(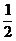 )x-1=
)x-1=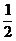
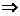 x=2.
x=2.
(2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0. ②
令t=4x-1,则方程②变为2t2-9t+4=0.
解得t1=4,t2=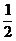 .
.
∴4x-1=4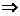 x=2,
x=2,
4x-1=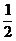
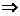 x=-
x=-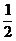 .
.
故方程另外两根是当a=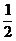 时,x=-1;
时,x=-1;
当a=4时,x=-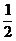 .
.
拓展应用 跳一跳,够得着!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com