14.命题“若m>0,则方程x²+x-m=0有实根”的逆命题为(　　 )

A.真　　　　　　　　　　 B.假　　　　　　 C.不确定　　　　　　　 D.以上都不对

答案：B

解析：其逆命题为“若方程x²+x-m=0有实根,则m>0”,由方程有实根,得Δ=1+4m>0,则m>-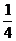,此时不一定有m>0,故逆命题不成立.

13.用反证法证明:若x²-(m+n)x+mn≠0,则x≠m且x≠n.

证明：假设x=m或x=n.

(1)当x=m时,则x²-(m+n)x+mn=0;

(2)当x=n时,则x²-(m+n)x+mn=0.

以上两种情况均与已知矛盾.

∴x≠m且x≠n.

拓展应用　 跳一跳，够得着！

12.已知m、n为实数,命题“若mn=0,则m=0或n=0”的否命题、逆否命题各是什么?命题“m²+n²=0,则m=0且n=0”的否命题、逆否命题各是什么?并判断以上各命题的真假.

解：“若mn=0,则m=0或n=0”的否命题是“若mn≠0,则m≠0且n≠0”;逆否命题是“若m≠0且n≠0,则mn≠0”.

命题“若m²+n²=0,则m=0且n=0”的否命题是“若m²+n²≠0,则m≠0或n≠0”;逆否命题是“若m≠0或n≠0,则m²+n²≠0”.

以上各命题都是真命题.

11.给出下列命题:

(1)命题“若b²-4ac<0,则方程ax²+bx+c=0(a≠0)无实根”的否命题;(2)命题“△ABC中,AB=BC=CA,那么△ABC为等边三角形”的逆命题;?(3)命题“若a>b>0,则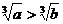>0”的逆否命题.

其中真命题的序号为__________________.

答案：①②③

解析：①若b²-4ac≥0,则方程ax²+bx+c=0(a≠0)有实根,正确.

②若△ABC为等边三角形,则有AB=BC=CA,正确.

③若≤≤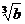0,则a≤b≤0,正确.

10.命题“若a>b,则ac>bc(a、b、c∈R)”与它的逆命题、否命题、逆否命题中,真命题的个数为__________________.

答案:0

解析：注意c∈R.

9.若命题p的否命题为r,命题r的逆命题为s,则s是p的逆命题t的(　　 )

A.逆否命题　　　　　　　　　　　　　　 B.逆命题

C.否命题　　　　　　　　　　 　　　　　D.原命题

答案：C

解析：由题知s是p的逆否命题,而t是p的逆命题,所以s是t的否命题.

8.一个命题与它的逆命题、否命题、逆否命题这四个命题中(　　 )

A.真命题的个数一定是奇数

B.真命题的个数一定是偶数

C.真命题的个数可能是奇数也可能是偶数

D.以上判断都不正确

答案：B

解析：原命题与逆否命题同真同假,逆命题与否命题同真同假.

7.给定命题:已知a、b为实数,若x²+ax+b≤0的解集是空集,则a²-4b≤0,写出它的逆命题、否命题、逆否命题,并判断四个命题的真假.

解：原命题:是假命题.逆命题:已知a、b为实数,若a²-4b≤0,则x²+ax+b≤0的解集是空集.假命题.否命题:已知a、b为实数,若x²+ax+b≤0的解集不是空集,则a²-4b>0.假命题.逆否命题:已知a、b为实数,若a²-4b>0,则x²+ax+b≤0的解集不是空集.假命题.

能力提升　 踮起脚,抓得住!

6.用反证法证明:“任何三角形至少有两个锐角”时,应假设_____________________.

答案：三角形至多有一个锐角

解析：即假设三角形只有一个锐角或一个锐角也没有.

5.“相似三角形的周长相等”写成“若p则q”的形式为_________________.

答案：若两三角形相似,则它们的周长相等

解析：条件p:若两三角形相似,结论q:它们的周长相等.