
题目列表(包括答案和解析)
4.下列命题中正确命题的个数是( )
(1)A∪B=B∪C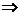 A=C (2)A∪B=B
A=C (2)A∪B=B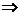 A∩B=A(3)a∈B
A∩B=A(3)a∈B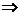 a∈B∩A
(4)A
a∈B∩A
(4)A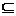 B
B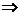 A∪B=B (5)a∈A
A∪B=B (5)a∈A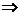 a∈A∪B
a∈A∪B
A.2 B.3
C.4 D.5
答案:B
解析:(1)不成立,如A、C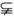 B未必A=C;(2)成立:A∪B=B
B未必A=C;(2)成立:A∪B=B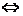 A
A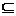 B
B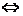 A∩B=A;(3)不成立,如a∈B,而a
A∩B=A;(3)不成立,如a∈B,而a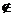 A,则a
A,则a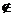 B∩A;(4)成立(见(2));(5)成立,因为A
B∩A;(4)成立(见(2));(5)成立,因为A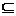 A∪B,其(2)(4)(5)正确.
A∪B,其(2)(4)(5)正确.
3.(2006甘肃兰州模拟)设全集U={0,-1,-2,-3,-4},集合M={0,-1,-2},N={0,-3,-4},那么(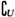 M)∩N为( )
M)∩N为( )
A.{-3,-4}
B.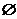 C.{-1,-2}
D.{0}
C.{-1,-2}
D.{0}
答案:A
解析: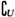 M={-3,-4},N={0,-3,-4},∴(
M={-3,-4},N={0,-3,-4},∴(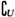 M)∩N={-3,-4}.
M)∩N={-3,-4}.
2.已知集合U为全集,集合M、N是集合U的真子集,若M∩N=N,则( )
A.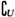 M
M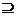
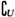 N B.M
N B.M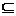
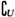 N
C.
N
C.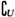 M
M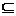
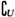 N D.
N D.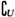 M
M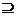
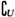 N
N
答案:C
解析:由M、N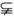 U且M∩N=N知N
U且M∩N=N知N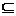 M
M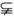 U,故
U,故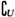 N
N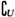 M.
M.
1.满足条件{0,1}∪A={0,1}的所有集合A的个数是( )
A.1 B.2 C.3 D.4
答案:D
解析:A可以是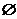 ,{0},{1},{0,1}.
,{0},{1},{0,1}.
16.已知f(x)=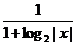 +p(p∈R).
+p(p∈R).
(1)试求f(x)的定义域;
(2)当x∈(-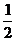 ,0)时,判断f(x)的单调性;
,0)时,判断f(x)的单调性;
(3)当x>0时,若f(x)的反函数为f-1(x),且f-1(0)的值在[2,3]之间,求p的取值范围.
解:(1)由1+log2|x|≠0,得x≠0且x≠±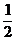 .
.
故所求定义域为(-∞,-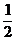 )∪(-
)∪(-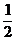 ,0)∪(0,
,0)∪(0,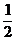 )∪(
)∪(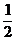 ,+∞).
,+∞).
(2)当x∈(-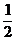 ,0)时,设x1、x2∈(-
,0)时,设x1、x2∈(-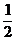 ,0)且x1<x2,
,0)且x1<x2,
则0<|x2|<|x1|<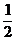 ,
,
log2|x2|<log2|x1|<-1.
∴1+log2|x2|<1+log2|x1|<0,
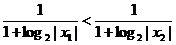 <0,
<0,
即f(x1)<f(x2).
故f(x)在(-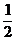 ,0)上单调递增.
,0)上单调递增.
(3)当x>0时,y=f(x)= 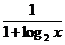 +p.
+p.
∴1+log2x=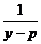 ,log2x=
,log2x=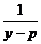 -1=
-1=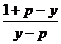 ,x=
,x=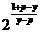 .
.
∴f-1(x)=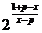 (x≠p),
(x≠p),
f-1(0)=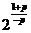 ∈[2,3],则1≤
∈[2,3],则1≤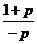 ≤log23.
≤log23.
解得-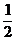 ≤p<-
≤p<-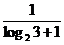 .
.
故p的取值范围为[-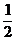 ,-
,-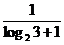 ].
].
15.已知y=loga(2-ax)在[0,1]上是关于x的减函数,则a的取值范围是( )
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
答案:B
解析:函数y=loga(2-ax)实际上是一次函数与对数函数的复合函数.
设u=2-ax.
则当0<a<1时,u是x的减函数,而函数y=logau是u的减函数,
故y=loga(2-ax)是x的增函数.
∴0<a<1不符合条件.∴a>1.
当x∈[0,1]时,u=2-ax>0,
当x=1时有2-a>0,从而a<2.
∴1<a<2.
14.函数y=logax,y=logbx,y=logcx,y=logdx的图象如图所示,则a、b、c、d的大小顺序是( )

A.1<d<c<a<b B.c<d<1<a<b
C.c<d<1<b<a D.d<c<1<a<b
答案:B
解析:由图象可知,当x=2时,
loga2>logb2>0>logc2>logd2,
即 .
.
∴lgb>lga>0>lgd>lgc.
解得b>a>1>d>c.
13.(1)若f(x)=lg(x2-2mx+1)的定义域为R,求实数m的取值范围;
(2)若f(x)=lg(x2-2mx+1)的值域为R,求实数m的取值范围.
解:(1)f(x)的定义域为R,即对任意的x∈R,f(x)恒有意义,即x2-2mx+1>0恒成立.
∴它所对应的函数g(x)=x2-2mx+1的图象都在x轴上方,故有Δ<0,即4m2-4<0.
∴-1<m<1.
(2)要使f(x)值域为R,需使u=x2-2mx+1取尽所有的正实数;
由u=x2-2mx+1的图象可知,只有在Δ≥0时才能满足要求,即4m2-4≥0,故m≥1或m≤-1.
拓展应用 跳一跳,够得着!
12.若f(x)=log4x+2(1≤x≤16),求y=f2(x)+f(x2)的值域.
解:先求f2(x)+f(x2)的定义域,
由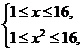 得1≤x≤4.
得1≤x≤4.
令t=log4x,则0≤t≤1.
y=(t+2)2+2t+2=t2+6t+6(0≤t≤1),
∴6≤y≤13,即值域为[6,13].
11.已知y=loga(x+1)(a>0,且a≠1)的值域为R,则x的取值范围是_____________.
答案:x>-1
解析:∵x+1要取遍一切正数,
∴x>-1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com