
题目列表(包括答案和解析)
14.设函数f(x)是(-∞,+∞)上的减函数,则f(2x-x2)的单调增区间是( )
A.(-∞,2) B.[-2,+∞] C.(-∞,-1] D.[1,+∞)
答案:D
解析:令t=g(x)=2x-x2=-(x-1)2+1知:当x≥1时,函数g(x)单调递减;当x≤1时,函数g(x)单调递增.又因函数f(t)在(-∞,+∞)上递减,故f(2x-x2)的单调减区间为(-∞,1],增区间为[1,+∞).
13.设函数f(x)对于任意x、y∈R,都有f(x+y)=f(x)+f(y),且f(x)在(-∞,+∞)上单调递减,若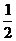 f(x2)-f(x)>
f(x2)-f(x)>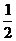 f(bx)-f(b),求x的范围.
f(bx)-f(b),求x的范围.
解:∵f(x+y)=f(x)+f(y)(x、y∈R),
∴2f(x)=f(x)+f(y)=f(2x).
同理,2f(b)=f(2b).
由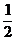 f(x2)-f(x)>
f(x2)-f(x)>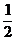 f(bx)-f(b),
f(bx)-f(b),
得f(x2)+2f(b)>f(bx)+2f(x),
即f(x2)+f(2b)>f(bx)+f(2x).
即f(x2+2b)>f(bx+2x).
又∵f(x)在(-∞,+∞)上单调递减,
∴x2+2b<bx+2x.
∴x2-(b+2)x+2b<0.
∴x2-(b+2)x+2b=(x-2)(x-b)<0.
当b>2时,得2<x<b;
当b<2时,得b<x<2;
当b=2时,得x∈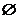 .
.
拓展应用 跳一跳,够得着!
12.证明函数f(x)=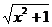 -x在其定义域内是减函数.
-x在其定义域内是减函数.
证明:∵函数f(x)的定义域为(-∞,+∞),
设x1、x2为区间(-∞,+∞)上的任意两个值且x1<x2,则f(x1)=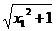 -x1,f(x2)=
-x1,f(x2)= -x2,
-x2,
f(x2)-f(x1)=  -
-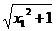 -(x2-x1)=
-(x2-x1)=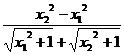 -(x2-x1)
-(x2-x1)
=(x2-x1)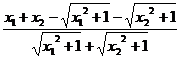 =(x2-x1)·
=(x2-x1)·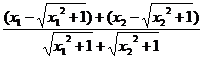 .
.
∵x2>x1,∴x2-x1>0且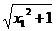 +
+ >0.
>0.
又∵对任意x∈R,都有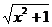 >
>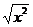 =|x|≥x,∴有
=|x|≥x,∴有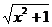 >x,即有x-
>x,即有x-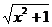 <0.
<0.
∴x1-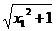 <0,x2-
<0,x2- <0.
<0.
∴f(x2)-f(x1)<0,即f(x2)<f(x1).
∴函数f(x)=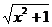 -x在其定义域R内单调递减.
-x在其定义域R内单调递减.
11.函数f(x)=|x2-2x-3|的增区间是_________________.
答案:(-1,1),(3,+∞)

解析:f(x)=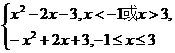 画出图象易知.
画出图象易知.
10.已知函数f(x)=x3-x在(0,a]上递减,在[a,+∞)上递增,则a=____________
答案: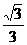
解析:设0<x1<x2<+∞,
f(x1)-f(x2)=(x1-x2)(x12+x1x2+x22-1),
当0<x1<x2≤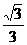 时,x1-x2<0,x12+x1x2+x22-1<0,则f(x1)>f(x2).
时,x1-x2<0,x12+x1x2+x22-1<0,则f(x1)>f(x2).
同理,可证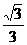 ≤x1<x2时,f(x1)<f(x2),故f(x)在(0,
≤x1<x2时,f(x1)<f(x2),故f(x)在(0,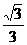 )上递减,在[
)上递减,在[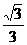 ,+∞]上递增,故?a=
,+∞]上递增,故?a=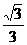 .
.
9.若f(x)=x2+bx+c,对任意实数t都有f(2+t)=f(2-t),那么( )
A.f(1)<f(2)<f(4) B.f(4)<f(2)<f(1)
C.f(2)<f(1)<f(4) D.f(2)<f(4)<f(1)
答案:C
解析:∵对称轴x=-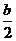 =2,∴b=-4.
=2,∴b=-4.
∴f(1)=f(3)<f(4).
8.设函数f(x)在(-∞,+∞)上是减函数,则下列不等式正确的是( )
A.f(2a)<f(a) B.f(a2)<f(a)
C.f(a2+a)<f(a) D.f(a2+1)<f(a)
答案:D
解析:∵a2+1-a=(a-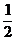 )2+
)2+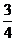 >0,
>0,
∴a2+1>a.函数f(x)在(-∞,+∞)上是减函数.
∴f(a2+1)<f(a).
7.定义在R上的函数f(x)满足f(-x)=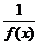 >0,又g(x)=f(x)+c(c为常数),在[a,b]上是单调递增函数,判断并证明g(x)在[-b,-a]上的单调性.
>0,又g(x)=f(x)+c(c为常数),在[a,b]上是单调递增函数,判断并证明g(x)在[-b,-a]上的单调性.
解:任取x1、x2∈[-b,-a]且-b≤x1<x2≤-a,
则g(x1)-g(x2)=f(x1)-f(x2)=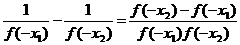 .
.
∵g(x)=f(x)+c在[a,b]上是增函数,
∴f(x)在[a,b]上也是增函数.
又b≥-x1>-x2≥a,
∴f(-x1)>f(-x2).
又f(-x1),f(-x2)皆大于0,∴g(x1)-g(x2)<0,即g(x1)<g(x2).故g(x)在[-b,-a]上是单调增函数.
能力提升 踮起脚,抓得住!
6.函数f(x)在定义域[-1,1]上是增函数,且f(x-1)<f(x2-1),则x的取值范围是_____________.
答案:1<x≤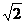
解析:依题意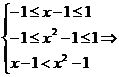 1<x≤
1<x≤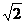 .
.
5.函数y=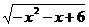 的单调递增区间是___________,单调递减区间是_____________.
的单调递增区间是___________,单调递减区间是_____________.
答案:[-3,-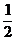 ] [-
] [-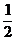 ,2]
,2]
解析:由-x2-x-6≥0,即x2+x-6≤0,解得-3≤x≤2.
∴y=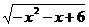 的定义域是[-3,2].
的定义域是[-3,2].
又u=-x2-x+6的对称轴是x=-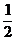 ,
,
∴u在x∈[-3,-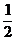 ]上递增,在x∈[-
]上递增,在x∈[-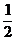 ,2]上递减.
,2]上递减.
又y=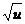 在[0,+∞]上是增函数,∴y=
在[0,+∞]上是增函数,∴y=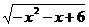 的递增区间是[-3,-
的递增区间是[-3,-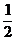 ],递减区间[-
],递减区间[-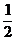 ,2].
,2].
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com