
题目列表(包括答案和解析)
2.设地球的半径为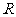 ,若在东经
,若在东经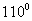 的经线上有北纬
的经线上有北纬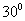 的点A和南纬
的点A和南纬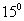 的点B,则A、B两点的球面距离是
的点B,则A、B两点的球面距离是
(A)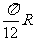 (B)
(B)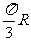 (C)
(C)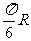 (D)
(D)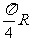
1.集合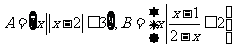 ,则
,则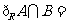
(A)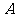 (B)
(B)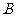 (C)
(C)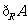 (D)
(D)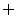
22. (本大题满分14分)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
AB=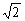 ,AF=1,M是线段EF的中点.
(1)求证AM∥平面BDE;
(2)求二面角A-DF-B的大小;
,AF=1,M是线段EF的中点.
(1)求证AM∥平面BDE;
(2)求二面角A-DF-B的大小;
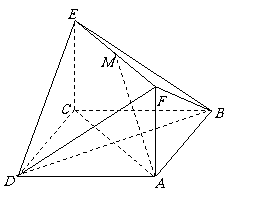 (3)试在线段AC上确定一点P,使得PF与CD所成的角是60°.
(3)试在线段AC上确定一点P,使得PF与CD所成的角是60°.
21.
(本大题满分12分)如图,设ABCDEF为正六边形,一只青蛙从顶点A开始随机跳动,每次随机地跳到与它所在顶点相邻的两顶点之一,每次按顺时针方向跳动的概率为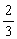 .
(1)求青蛙从A点开始经过3次跳动所处的位置为D点概率;
(2)求青蛙从A点开始经过4次跳动所处的位置为E点概率.
.
(1)求青蛙从A点开始经过3次跳动所处的位置为D点概率;
(2)求青蛙从A点开始经过4次跳动所处的位置为E点概率.

20.
(本大题满分12分)如图,ABCD为矩形,PA⊥平面ABCD,M、N分别是AB、PC中点.
(1)求证:MN⊥AB;
(2)若平面PDC与底面ABC所成角为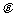 ,能否确定
,能否确定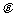 ,使MN是异面直线AB与PC的公
,使MN是异面直线AB与PC的公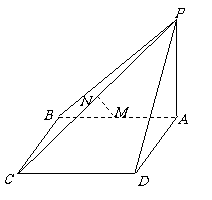 垂线,若能求出
垂线,若能求出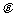 ;若不能说明理由.
;若不能说明理由.
19. (本大题满分12分)某网络安全中心同时对甲、乙、丙三个网络系统的安全进行监控,以便在发现黑客入侵时及时跟踪锁定.今测得在一段时间内,甲、乙、丙三个网络系统各自遭受到黑客入侵的概率分别为0.1、0.2、0.15. (1)求三个网络系统都受到黑客入侵的概率; (2)求只有一个网络系统受到黑客入侵的概率.
18.
(本大题满分12分)已知平面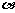 ∥平面
∥平面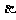 ,直线a与平面
,直线a与平面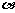 相交,求证:直线a与平面
相交,求证:直线a与平面 相交.
相交.
17.
(本大题满分12分)已知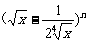 的展开式中,前三项系数的绝对值依次成等差数列.
(1)证明:展开式中没有常数项;
(2)求展开式中所有有理项.
的展开式中,前三项系数的绝对值依次成等差数列.
(1)证明:展开式中没有常数项;
(2)求展开式中所有有理项.
16. 设l、m、n是三条不同的直线, 是三个不同的平面,下面有四个命题:
①若l∥
是三个不同的平面,下面有四个命题:
①若l∥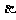 ,
,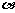 ∥
∥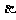 ,则l∥
,则l∥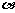 ②l∥n,m∥n,则l∥m
③若
②l∥n,m∥n,则l∥m
③若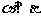 ,l∥
,l∥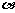 ,则
,则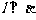 ④若
④若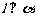 ,
,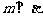 ,
,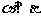 ,则l⊥m
其中正确命题的序号有 .
,则l⊥m
其中正确命题的序号有 .
15. 口袋中有红球2个,黑球3个,白球5个,它们只有颜色不同.从中摸出四个,摸出的球中同色的两个为一组,若红色一组得5分,黑色一组得3分,白色一组得1分,则得分总数取得最大值的概率为________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com