
题目列表(包括答案和解析)
7.经过点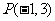 ,且与向量
,且与向量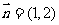 垂直的直线
垂直的直线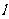 的点法向量式方程为
.
的点法向量式方程为
.
6.已知点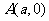 与
与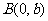 ,且
,且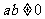 .则
.则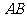 所在直线
所在直线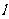 的点方向式方程为
.
的点方向式方程为
.
5.一架飞机向东飞行100千米,然后改变方向向南飞行100千米,则这架飞机两次位移的和为 .(精确到千米)
4.若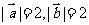 ,且
,且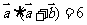 ,则向量
,则向量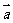 与
与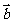 的夹角为 .
的夹角为 .
3.已知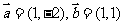 ,若
,若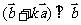 ,则实数
,则实数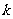 的值为 .
的值为 .
2.若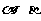 是某三角形的两个内角,且行列式
是某三角形的两个内角,且行列式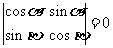 ,则
,则 的值为 .
的值为 .
1.若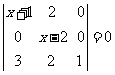 ,则
,则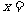 .
.
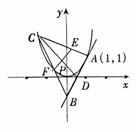
20.解一:过抛物线上点A的切线斜率为: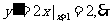 切线AB的方程为
切线AB的方程为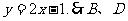 的坐标为
的坐标为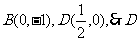 是线段AB的中点.
是线段AB的中点.
设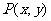 、
、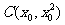 、
、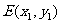 、
、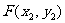 ,则由
,则由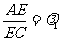 知,
知,
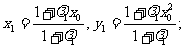
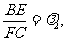 得
得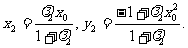
 ∴EF所在直线方程为:
∴EF所在直线方程为: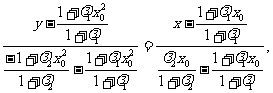
化简得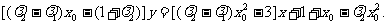
当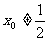 时,直线CD的方程为:
时,直线CD的方程为: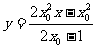 …②
…②
联立①、②解得 ,消去
,消去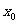 ,得P点轨迹方程为:
,得P点轨迹方程为: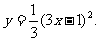
当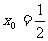 时,EF方程为:
时,EF方程为: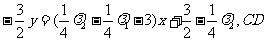 方程为:
方程为: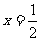 ,联立解得
,联立解得 也在P点轨迹上.因C与A不能重合,∴
也在P点轨迹上.因C与A不能重合,∴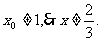
∴所求轨迹方程为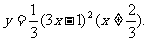
解二:由解一知,AB的方程为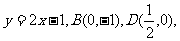 故D是AB的中点.
故D是AB的中点.
令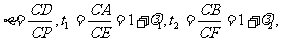 则
则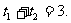 因为CD为
因为CD为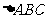 的中线,
的中线,
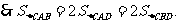
而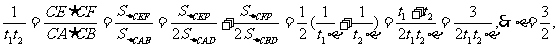
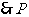 是
是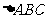 的重心.
的重心.
设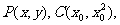 因点C异于A,则
因点C异于A,则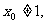 故重心P的坐标为
故重心P的坐标为
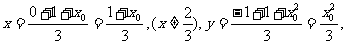 消去
消去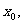 得
得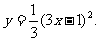
故所求轨迹方程为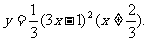
19. 解:(Ⅰ)直线AB、AC、BC的方程依次为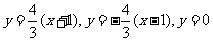 。点
。点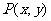 到AB、AC、BC的距离依次为
到AB、AC、BC的距离依次为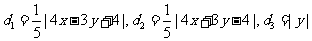 。依设,
。依设,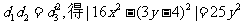 ,即
,即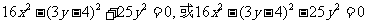 ,化简得点P的轨迹方程为
,化简得点P的轨迹方程为
圆S: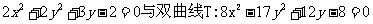
(Ⅱ)由前知,点P的轨迹包含两部分
圆S: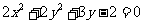 ①
①
与双曲线T: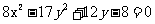 ②
②
因为B(-1,0)和C(1,0)是适合题设条件的点,所以点B和点C在点P的轨迹上,且点P的轨迹曲线S与T的公共点只有B、C两点。
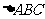 的内心D也是适合题设条件的点,由
的内心D也是适合题设条件的点,由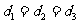 ,解得
,解得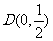 ,且知它在圆S上。直线L经过D,且与点P的轨迹有3个公共点,所以,L的斜率存在,设L的方程为
,且知它在圆S上。直线L经过D,且与点P的轨迹有3个公共点,所以,L的斜率存在,设L的方程为
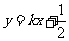 ③
③
(i)当k=0时,L与圆S相切,有唯一的公共点D;此时,直线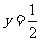 平行于x轴,表明L与双曲线有不同于D的两个公共点,所以L恰好与点P的轨迹有3个公共点。......10分
平行于x轴,表明L与双曲线有不同于D的两个公共点,所以L恰好与点P的轨迹有3个公共点。......10分
(ii)当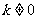 时,L与圆S有两个不同的交点。这时,L与点P的轨迹恰有3个公共点只能有两种情况:
时,L与圆S有两个不同的交点。这时,L与点P的轨迹恰有3个公共点只能有两种情况:
情况1:直线L经过点B或点C,此时L的斜率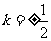 ,直线L的方程为
,直线L的方程为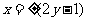 。代入方程②得
。代入方程②得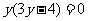 ,解得
,解得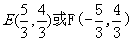 。表明直线BD与曲线T有2个交点B、E;直线CD与曲线T有2个交点C、F。
。表明直线BD与曲线T有2个交点B、E;直线CD与曲线T有2个交点C、F。
故当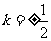 时,L恰好与点P的轨迹有3个公共点。
时,L恰好与点P的轨迹有3个公共点。
情况2:直线L不经过点B和C(即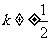 ),因为L与S有两个不同的交点,所以L与双曲线T有且只有一个公共点。即方程组
),因为L与S有两个不同的交点,所以L与双曲线T有且只有一个公共点。即方程组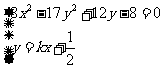 有且只有一组实数解,消去y并化简得
有且只有一组实数解,消去y并化简得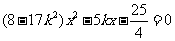
该方程有唯一实数解的充要条件是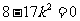 ④
④
或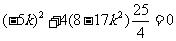 ⑤
⑤
解方程④得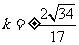 ,解方程⑤得
,解方程⑤得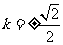 。
。
综合得直线L的斜率k的取值范围是有限集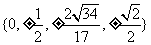 。 .
。 .
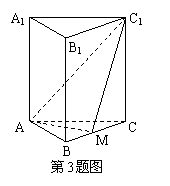
18.证(Ⅰ)∵ABCD-A1B1C1D1是正四棱柱,
∴D1D⊥ABCD.
连AC,又底面ABCD是正方形,
∴AC⊥BD,
由三垂线定理知 D1B⊥AC.
同理,D1B⊥AE,AE∩AC = A,
∴D1B⊥平面AEC .
解(Ⅱ)VB-AEC = VE-ABC .
∵EB⊥平面ABC,
∴EB的长为E点到平面ABC的距离.
∵Rt△ABE ~ Rt△A1AB,
∴EB
=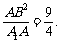
∴VB-AEC = VE-ABC =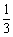 S△ABC·EB
S△ABC·EB
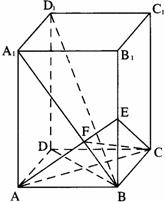
=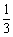 ×
×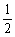 ×3×3×
×3×3×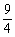
=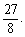 (10分)
(10分)
解(Ⅲ)连CF,
∵CB⊥平面A1B1BA,又BF⊥AE,
由三垂线定理知,CF⊥AE .
于是,∠BFC为二面角B-AE-C的平面角,
在Rt△ABE中,BF =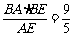 ,
,
在Rt△CBF中,tg∠BFC =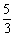 ,
,
∴∠BFC
= arctg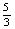 .
.
 即二面角B-AE-C的大小为arctg
即二面角B-AE-C的大小为arctg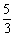 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com