18．如图，已知正四棱柱ABCD-A₁B₁C₁D₁的底面边长为3，侧棱长为4，连结A₁B，过A作AF⊥A₁B垂足为F，且AF的延长线交B₁B于E。

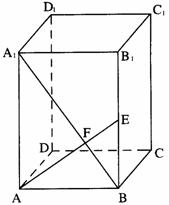
(Ⅰ)求证：D₁B⊥平面AEC；

(Ⅱ)求三棱锥B-AEC的体积；

(Ⅲ)求二面角B-AE-C的大小.

17．设曲线C₁: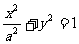(a为正常数)与C₂:y²=2(x+m)在x轴上方公有一个公共点P。

(1)实数m的取值范围(用a表示)；

(2)O为原点，若C₁与x轴的负半轴交于点A，当0<a<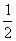时，试求⊿OAP的面积的最大值(用a表示)。

16．把椭圆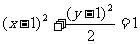绕它的中心旋转90°，再沿x轴方向平行移动，使变换后的椭圆截直线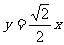所得线段长为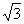，求变换后的椭圆方程。

15．求过原点且与直线x=1 及圆(x-1)²+(y-2)²=1均相切的圆的方程。

14．对于四面体ABCD，给出下列四个命题：①若AB=AC，BD=CD则BC⊥AD；②若AB=CD，AC=BD则BC⊥AD；③若AB⊥AC，BD⊥CD则BC⊥AD；④若AB⊥CD， BD⊥AC则BC⊥AD；其中真命题序号是　　　　　 ．

13．若正方形ABCD的一条边在直线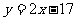上，另外两个顶点在抛物线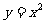上.则该正方形面积的最小值为　　　 　.

12．设F₁，F₂是椭圆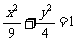的两个焦点，P是椭圆上的点，且|PF₁| : |PF₂|＝2 : 1，则三角形PF₁F₂的面积等于______________．

11．在椭圆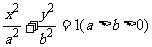中，记左焦点为F，右顶点为A，短轴上方的端点为B。若该椭圆的离心率是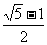，则=　　　　　　　 　　　。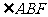

10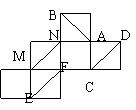．有一正方提纸盒展开如图，在原正方体纸盒中有如下结论：①AB⊥EF②AB和CM成60°③EF和MN为异面直线④MN∥CD，其中正确序号是　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．①②

B．③④

C．②③

D．①③

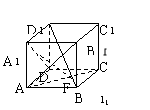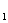9．如图，正方体ABCD-ABCD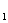中，EF是异面直线AC和A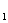D的公垂线，则EF和BD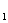关系是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　　 )

　　 A．相交不垂直　　　　　　 B．相交垂直

　　 C．异面直线　　　　　　　 D．互相平行