
1.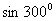 = ( )
= ( )
A.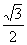 B.
B.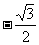 C.
C.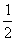 D.
D.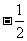
22.(本题满分14分)
已知函数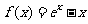 (
(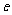 为自然对数的底数).
为自然对数的底数).
(1)求 的最小值;
的最小值;
(2)不等式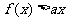 的解集为
的解集为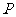 ,若
,若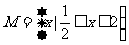 且
且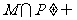 求实数
求实数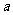 的取值范围;
的取值范围;
(3)已知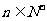 ,且
,且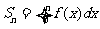 ,是否存在等差数列
,是否存在等差数列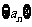 和首项为
和首项为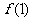 公比大于0的等比数列
公比大于0的等比数列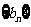 ,使得
,使得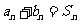 .若存在,请求出数列
.若存在,请求出数列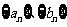 的通项公式.若不存在,请说明理由.
的通项公式.若不存在,请说明理由.
21.(本题满分12分)
设椭圆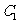 、抛物线
、抛物线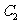 的焦点均在
的焦点均在 轴上,
轴上,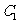 的中心和
的中心和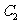 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
|
x |
3 |
-2 |
4 |
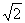 |
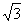 |
|
y |
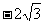 |
0 |
-4 |
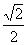 |
-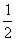 |
(1)求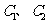 的标准方程;
的标准方程;
(2)设直线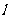 与椭圆
与椭圆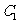 交于不同两点
交于不同两点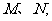 且
且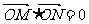 ,请问是否存在这样的直线
,请问是否存在这样的直线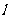 过抛物线
过抛物线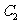 的焦点
的焦点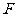 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
20.(本题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数.并说明它在乙组数据中的含义;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为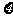 ,求
,求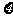 的分布列及数学期望
的分布列及数学期望
19.(本题满分12分)
如下图的多面体是底面为平行四边形的直四棱柱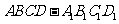 ,经平面
,经平面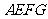 所截后得到的图形.其中
所截后得到的图形.其中 ,
,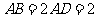 ,
,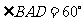 .
.
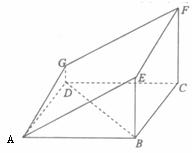
(1)求证: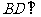 平面
平面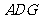 ;
;
(2)求平面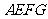 与平面
与平面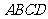 所成锐二面角的余弦值.
所成锐二面角的余弦值.
18.(本题满分12)
已知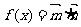 ,其中
,其中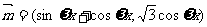 ,
,
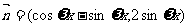 (
( ).若
).若 图象中相邻的对称轴间的距离不小于
图象中相邻的对称轴间的距离不小于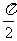 .
.
(1)求 的取值范围
的取值范围
(2)在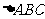 中,
中,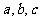 分别为角
分别为角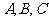 的对边.且
的对边.且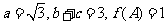 ,当
,当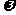 最大时.求
最大时.求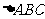 面积.
面积.
17.(本题满分12)
设非负实数 、
、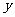 满足不等式组
满足不等式组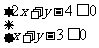
(1)如下图在所给的坐标系中,画出不等式组所表示的平面区域;
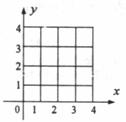
(2)求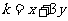 的取值范围;
的取值范围;
(3)在不等式组所表示的平面区域内,求点(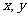 )落在
)落在 ∈[1,2]区域内的概率.
∈[1,2]区域内的概率.
16.设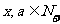 ,且关于不等式
.
,且关于不等式
.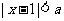 的解集有且仅有5个元素.则
的解集有且仅有5个元素.则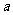 的值是
.
的值是
.
15.对任意非零实数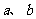 .若
.若 的运算原理如下图所示.则
的运算原理如下图所示.则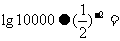 .
.
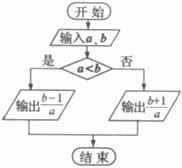
14.若函数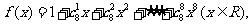 则
则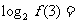 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com