
19.(本小题满分14分)
如图,已知定圆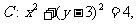 定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线m相交于N,与圆C相交于P、Q两点,M是PQ中点。
定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线m相交于N,与圆C相交于P、Q两点,M是PQ中点。
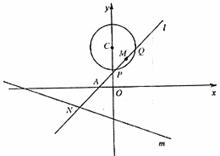
(I)当e与m垂直时,求证:l过圆心C;
(II)当|PQ|=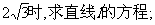
(III)设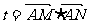 ,试问t是否为定值,若为定值,请求出t的值;若不为定值,请说明理由。
,试问t是否为定值,若为定值,请求出t的值;若不为定值,请说明理由。
18.(本小题满分13分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,根据以往的统计数据,甲、乙射击环数的频率分布条形图如下:
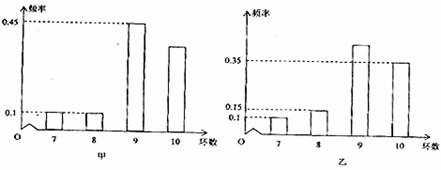
若将频率视为概率,回答下列问题:
(I)若甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(II)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及数学期望Eξ.
17.(本小题满分14分)
如图,ABCD是边长为2a的正方形,ABEF是矩形,且二面角C-AB-F是直二面角,AF=a,G是EF的中点。
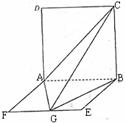
(I)求证:平面AGC⊥平面BGC;
(II)求CB与平面AGC所成角的大小;
(III)求二面角B-AC-G的大小.
16.(本小题满分13分)
在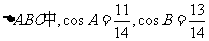 .
.
(I)求cosC的值;
(II)若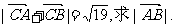
15.(本小题满分13分)
已知递增的等比数列{an}满足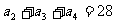 ,且a3+2是a2,a4的等差中项。
,且a3+2是a2,a4的等差中项。
(I)求数列{an}的通项公式;
(II)若bn=log2an+1,Sn是数列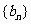 的前n项和,求使
的前n项和,求使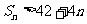 成立的n最小值.
成立的n最小值.
14.已知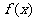 是奇数,且对定义域内任意自变量x满足
是奇数,且对定义域内任意自变量x满足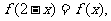 当
当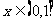 时,
时,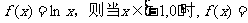 ;当
;当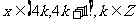 时,f(x)= .
时,f(x)= .
13.已知正三棱锥P-ABC的四个顶点都在同一球面上,其中底面的三个顶点在该球的一个大圆上,若正三棱锥高为1,则球的半径为 ,P、A两点的球面积距离为 .
12.关于函数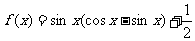 给出下列三个命题:
给出下列三个命题:
(1)函数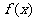 在区间
在区间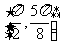 上是减函数;
上是减函数;
(2)直线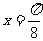 是函数
是函数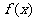 的图象的一条对称轴;
的图象的一条对称轴;
(3)函数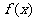 的图象可以由函数
的图象可以由函数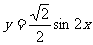 的图象向左平移
的图象向左平移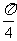 而得到.
而得到.
其中正确的命题序号是 .(将你认为正确命题序号都填上)
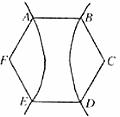
11.如图,已知ABCDEF为正六边形,若以G、F为焦点的双曲线恰好经过A,B,D,E四点,则该双曲线的离心率为 。
10.若二项式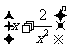 的展开式共7项,则展开式中的常数项为
。
的展开式共7项,则展开式中的常数项为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com