
22.(本题12分)已知:椭圆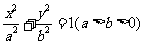 的离心率为
的离心率为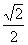 ,其右顶点为A,上顶点为B,左右焦点分别为F1,F2,且
,其右顶点为A,上顶点为B,左右焦点分别为F1,F2,且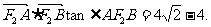
(Ⅰ)求椭圆的方程;
(Ⅱ)在线段AB上(不包括端点)是否存在点M,使∠F1MF2为直角?若存在,求出点M的坐标;若不存在,说明理由。
21.(本题12分)已知函数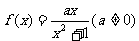
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=2,判断直线3x-y+m=0是不是函数f(x)的图像的切线,若是,求出实数m的值;若不是,说明理由。
20.(本题12分)已知数列{an}满足an==2 an-1+2n-1(n∈N*,n 2),且a4=81.
2),且a4=81.
(Ⅰ)求数列{an}的前三项a1、a2、a3的值;
(Ⅱ)是否存在一个实数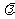 ,使得数列
,使得数列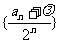 为等差数列?若存在,求出
为等差数列?若存在,求出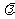 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(Ⅲ)求数列{an}的前n项和Sn。
19.(本题12分)如下图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC成60°角。
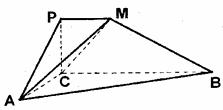
(Ⅰ)求证:平面PAC⊥平面ABC;
(Ⅱ)求二面角M-AC-B的大小;
18.(本小题12分)
某安全生产监督部门对4家小型煤矿进行监察,若安检不合格,则必须整改,若整改后经复查仍不合格,则强制关闭,设每家煤矿安检是否合格相互独立,且每家煤矿整改前安检合格的概率是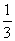 ,整改后安检合格的概率是
,整改后安检合格的概率是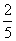 。
。
(1)求恰好有两家煤矿必须整改的概率;
(2)设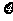 为关闭煤矿的个数,求
为关闭煤矿的个数,求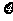 的分布列和数学期望E
的分布列和数学期望E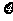 。
。
17.(本题10分)已知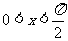 ,函数
,函数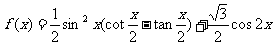 。
。
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)= 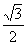 ,求x的取值集合。
,求x的取值集合。
16.已知球O的半径是1,A、B、C三点都在球面上,A、B两点和A、C两点的球面距离都是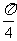 ,B、C两点的球面距离是
,B、C两点的球面距离是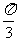 ,则二面角B-OA-C的大小是
。
,则二面角B-OA-C的大小是
。
15.若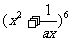 的二项展开式中
的二项展开式中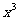 的系数为
的系数为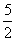 ,则a=
(用数字作答)。
,则a=
(用数字作答)。
14.若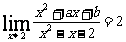 ,则
,则 =
。
=
。
13.已知随机变量 服从正态分布N(2,
服从正态分布N(2,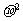 ),P(
),P( )=0.84,则P(
)=0.84,则P(
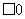 )= 。
)= 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com