
18.(本小题共14分)
某校高二年级开设《几何证明选讲》及《数学史》两个模块的选修科目。每名学生至多选修一个模块,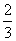 的学生选修过《几何证明选讲》,
的学生选修过《几何证明选讲》,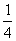 的学生选修过《数学史》,假设各人的选择相互之间没有影响。
的学生选修过《数学史》,假设各人的选择相互之间没有影响。
(I)任选一名学生,求该生没有选修过任何一个模块的概率;
(II)任选4名学生,求至少有3人选修过《几何证明选讲》的概率。
17.(本小题共14分)
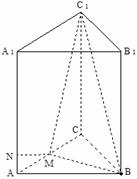
如图,在正三棱柱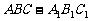 中,
中,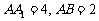 ,
,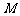 是
是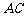 的中点,点
的中点,点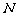 在
在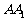 上,
上,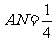 。
。
(Ⅰ)求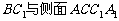 所成角的大小;
所成角的大小;
(Ⅱ)求二面角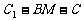 的正切值;
的正切值;
(Ⅲ)证明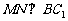 .
.
16.(本小题共13分)
已知数列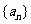 中,
中,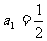 ,点(1,0)在函数
,点(1,0)在函数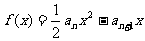 的图像上。
的图像上。
(Ⅰ)求数列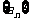 的通项;
的通项;
(Ⅱ)设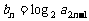 ,求数列
,求数列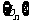 的前n项和
的前n项和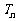 。
。
15.(本小题共13分)
|
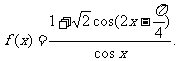
(Ⅰ)求函数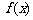 的定义域;
的定义域;
(Ⅱ)求函数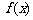 在区间
在区间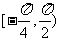 上的最值。
上的最值。
14.对于函数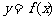 ,我们把使
,我们把使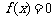 的实数x叫做函数
的实数x叫做函数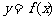 的零点。函数
的零点。函数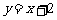 的零点是 ;若函数
的零点是 ;若函数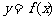 和
和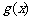 均是定义在
均是定义在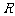 上的连续函数,且部分函数值分别由下表给出:
上的连续函数,且部分函数值分别由下表给出:

则当x= 时,函数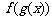 在区间
在区间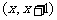 上必有零点。
上必有零点。
13.在平面直角坐标系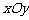 中,已知△
中,已知△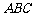 顶点
顶点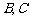 分别为椭圆
分别为椭圆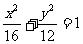 的两个焦点,顶点
的两个焦点,顶点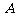 在该椭圆上,则
在该椭圆上,则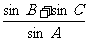 =
。
=
。
12.在长方体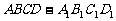 中,
中,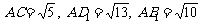 ,则长方体的对角线长为 。
,则长方体的对角线长为 。
11.设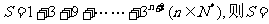 。
。
10.若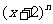 展开式的二项式系数之和等于64,则第三项是
。
展开式的二项式系数之和等于64,则第三项是
。
9.不等式 的解集是
。
的解集是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com