
2.已知i是虚数单位,复数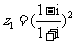 、
、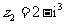 分别对应复平面上的点
分别对应复平面上的点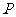 、
、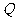 ,则向量
,则向量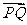 对应的复数是( )
对应的复数是( )
A.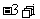 B.
B. C.
C. D.
D.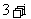
1.已知全集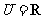 ,
,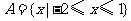 ,
, ,
,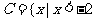 或
或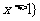 ,
,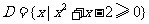 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.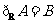 B.
B. 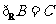 C.
C.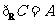 D.
D. 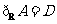
24.(本小题满分10分)选修4-5:不等式选讲
已知函数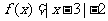 ,
,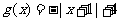 .
.
(Ⅰ)若函数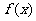 的值不大于1,求
的值不大于1,求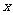 的取值范围;
的取值范围;
(Ⅱ)若不等式 的解集为R,求
的解集为R,求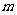 的取值范围.
的取值范围.
23.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系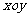 中,曲线
中,曲线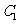 的参数方程为
的参数方程为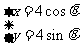 (
(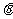 为参数,且
为参数,且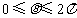 ),点
),点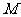 是曲线
是曲线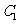 上的动点.
上的动点.
(Ⅰ)求线段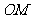 的中点
的中点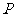 的轨迹的直角坐标方程;
的轨迹的直角坐标方程;
(Ⅱ)以坐标原点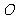 为极点,
为极点,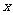 轴的正半轴为极轴建立极坐标系,若直线
轴的正半轴为极轴建立极坐标系,若直线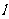 的极坐标方程为
的极坐标方程为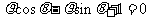 (
( ),求点
),求点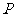 到直线
到直线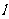 距离的最大值.
距离的最大值.
22.(本小题满分10分)选修4-1:几何证明选讲
如图,⊙O是以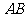 为直径的△ABC的外接圆,点
为直径的△ABC的外接圆,点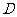 是劣弧
是劣弧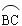 的中点,连结
的中点,连结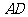 并延长,与过
并延长,与过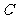 点的切线交于
点的切线交于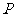 ,
,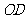 与
与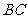 相交于点
相交于点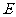 .
.
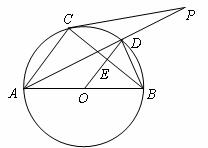
(Ⅰ)求证: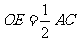 ;
;
(Ⅱ)求证: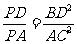 .
.
21.(本小题满分12分)
已知函数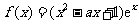 ,(
,(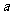 为常数,
为常数,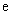 为自然对数的底).
为自然对数的底).
(Ⅰ)求函数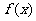 的单调区间;
的单调区间;
(Ⅱ)若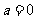 ,且经过点
,且经过点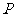 (0,
(0,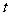 )(
)(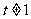 )有且只有一条直线与曲线
)有且只有一条直线与曲线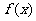 相切,求
相切,求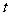 的取值范围.
的取值范围.
※考生注意:请在第22、23、24题中任选一题做答,如果多做,则在所做的题中,按题号顺序的第一题记分。
20.(本小题满分12分)
设椭圆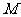 :
: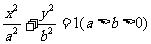 的离心率为
的离心率为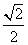 ,点
,点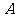 (
(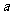 ,0),
,0),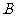 (0,
(0, ),原点
),原点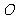 到直线
到直线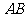 的距离为
的距离为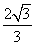 .
.
(Ⅰ)求椭圆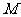 的方程;
的方程;
(Ⅱ)设直线 :
: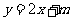 与椭圆
与椭圆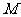 相交于
相交于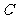 、
、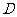 不同两点,经过线段
不同两点,经过线段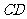 上点
上点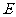 的直线与
的直线与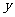 轴相交于点
轴相交于点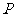 ,且有
,且有 ,
,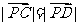 ,试求
,试求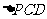 面积
面积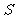 的最大值.
的最大值.
19.(本小题满分12分)
国际标准游泳池长50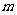 ,宽至少21
,宽至少21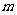 ,深1.80
,深1.80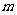 以上,设8条泳道,每条泳道宽2.50
以上,设8条泳道,每条泳道宽2.50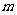 ,分道线由直径5-10
,分道线由直径5-10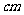 的单个浮标连接而成.某位游泳教练员指导甲、乙两名游泳运动员在这样国际标准的游泳池内同时进行游泳训练,甲、乙两名运动员可以随机的选择不同的泳道进行训练.
的单个浮标连接而成.某位游泳教练员指导甲、乙两名游泳运动员在这样国际标准的游泳池内同时进行游泳训练,甲、乙两名运动员可以随机的选择不同的泳道进行训练.
(Ⅰ)求甲、乙两名运动员选择的泳道相隔数的分布列和期望;
(Ⅱ)若教练员为避免甲、乙两人训练的相互干扰,要求两人相隔的泳道数不少于2,为了同时计时的方便,又要求两人相隔的泳道数不能超过4,求甲、乙两名运动员随机的选择不同的泳道训练恰好符合教练员的要求的概率.
18.(本小题满分12分)
如下图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=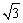 , AA1=3,M为侧棱CC1上一点,
, AA1=3,M为侧棱CC1上一点,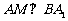 .
.
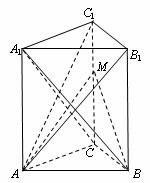
(Ⅰ)求证:AM^平面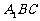 ;
;
(Ⅱ)求平面ABM与平面AB1C1所夹锐角的余弦值.
17.(本小题满分12分)
已知各项为正数的数列{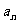 }满足
}满足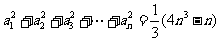 ,(
,(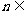 N*).
N*).
(Ⅰ)求数列{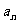 }的前
}的前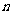 项和
项和 ;
;
(Ⅱ)记数列{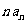 }的前
}的前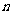 项和为
项和为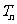 ,试用数学归纳法证明对任意
,试用数学归纳法证明对任意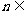 N*,都有
N*,都有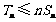 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com